题目内容
如图,过点B(0,-b)作椭圆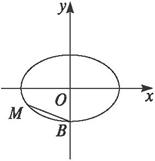
解:设M(x,y)是椭圆上任一点.
|BM|2=x2+(y+b)2=x2+y2+2by+b2,
由![]() +
+![]() =1,有x2=
=1,有x2=![]() (b2-y2).
(b2-y2).
将其代入上式,整理,然后配方有
|BM|2=(1-![]() )y2+2by+(a2+b2)=(1-
)y2+2by+(a2+b2)=(1-![]() )·(y-
)·(y-![]() )2+
)2+![]() .
.
∵-b≤y≤b,
(1)当b≤c(即b≤![]() a)时,
a)时,![]() ≤b,∴y=
≤b,∴y=![]() 时,|BM|的最大值为
时,|BM|的最大值为![]() ;
;
(2)当b>c(b>![]() a)时,
a)时,![]() >b,故y=b时,点M在(0,b),即y轴上之顶点位置,|BM|2的最大值为(1-
>b,故y=b时,点M在(0,b),即y轴上之顶点位置,|BM|2的最大值为(1-![]() )(b-
)(b-![]() )2+
)2+![]() =4b2.
=4b2.
∴|BM|的最大值为2b.

练习册系列答案
相关题目
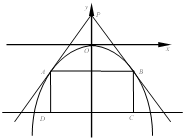 如图,过点P(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,且AD和BC均垂直于直线y=-8,垂足分别为D,C,得矩形ABCD.
如图,过点P(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,且AD和BC均垂直于直线y=-8,垂足分别为D,C,得矩形ABCD. (2012•温州一模)如图,过点A(0,-1)的动直线l与抛物线C:x2=4y交于P(x1,y1),Q(x2,y2)两点.
(2012•温州一模)如图,过点A(0,-1)的动直线l与抛物线C:x2=4y交于P(x1,y1),Q(x2,y2)两点. (2007•闸北区一模)如图:过点P(0,2)做直线交抛物线x2=2y于A,B两点,O为坐标原点.
(2007•闸北区一模)如图:过点P(0,2)做直线交抛物线x2=2y于A,B两点,O为坐标原点.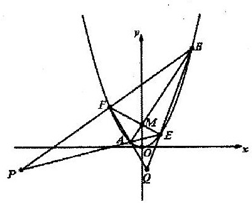 (2012•浙江模拟)己知抛物线C:x2=2py(p>0)上一点T(m,4)到其焦点的距离为
(2012•浙江模拟)己知抛物线C:x2=2py(p>0)上一点T(m,4)到其焦点的距离为