题目内容
如图所示，在正方体ABCD-A1B1C1D1中，AE=3EB；
（Ⅰ）若A1F=
FA，求证：EF∥面DD1C1C；
（Ⅱ） 求二面角A-EC-D1的正切值、
（Ⅰ）若A1F=
| 1 |
| 3 |
（Ⅱ） 求二面角A-EC-D1的正切值、
（Ⅰ）连A1B，∵AE=3EB.A1F=
FA
∴
=
=3，∴FE∥A1B，又D1C∥A1B
∴EF∥D1C，EF?面DD1C1C，D1C?面DD1C1C
∴FE∥面DD1C1C
（Ⅱ）过点D作DG⊥EC，连接D1G．
由DD1⊥平面ABCD得D1G⊥CE，又DG⊥EC，DG∩DD1=D，
∴CE⊥平面D1DG．∴CE⊥D1G，
∴∠D1GD就是二面角A-EC-D1的平面角．
设正方体ABCD-A1B1C1D1的棱长为4，则AE=3，EB=1．
CE=
=
，△DEC中，由等面积法，DG=
=
．
∴△D1DG中，tanD1GD=
=
=
．
∴二面角A-EC-D1的正切值为
| 1 |
| 3 |
∴
| AE |
| EB |
| AF |
| FA1 |
∴EF∥D1C，EF?面DD1C1C，D1C?面DD1C1C
∴FE∥面DD1C1C
（Ⅱ）过点D作DG⊥EC，连接D1G．
由DD1⊥平面ABCD得D1G⊥CE，又DG⊥EC，DG∩DD1=D，
∴CE⊥平面D1DG．∴CE⊥D1G，
∴∠D1GD就是二面角A-EC-D1的平面角．
设正方体ABCD-A1B1C1D1的棱长为4，则AE=3，EB=1．
CE=
| 42+1 |
| 17 |
| 4×4 | ||
|
| 16 | ||
|
∴△D1DG中，tanD1GD=
| DD1 |
| DG |
| 4 | ||||
|
| ||
| 4 |
∴二面角A-EC-D1的正切值为
| ||
| 4 |
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
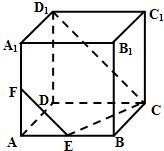如图所示，在正方体ABCD-A1B1C1D1中，E为AB的中点
（2011•宝山区二模）如图所示，在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等，则动点P所在曲线形状为（ ）
如图所示，在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等，则动点P所在曲线的形状为（ ）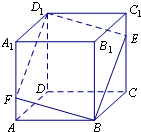
如图所示，在正方体ABCD-A1B1C1D1中，点E是棱CC1上的一个动点，平面BED1交棱AA1于点F．则下列命题中假命题是（ ）