Question

【题目】（1）已知当时，不等式恒成立，求实数的取值范围

（2）解关于的不等式.

Answer 1

【答案】（1）x=3（2）当时，解集为： ，当时，解集为：

【解析】试题分析：（1）将不等式转化为关于a的不等式，根据一次函数性质得不等式组，解不等式组可得实数的取值范围（2）分类讨论：由于a=0表示的为一次函数，a 为二次函数，那么分为两大类，结合开口方向和根的大小，和二次函数图形可知，需要整体分为a>0,a=0,a<0来求解，那么对于的大小将会影响到根的大小，所以要将a分为和，以及来得到结论，

试题解析:解：（1）原式可化为：

设

则为关于的一次函数，由题意：

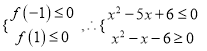
解得：

（2）原不等式可化为：

当时，原不等式的解集为：

当时，原不等式的解集为：

当时，原不等式的解集为：

当时，原不等式的解集为：

当时，原不等式的解集为：