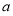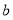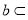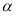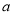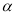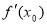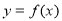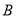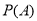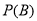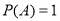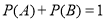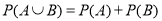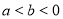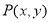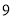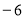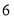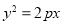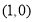题目内容
已知等比数列
中，
，
．
(1)求数列的通项公式；
(2)若
，
分别为等差数列
的第3项和第5项，试求数列
的通项公式及前
项和
．
(1) 
；(2) 
，
.
【解析】
试题分析：(1) 设等比数列
的公比为
,由
求出公比的值,从而得到等比数列的通项公式.
(2)首先根据(1)所得通项公式求出
，
,从而得出等差数列
的第3项
和第5项
.
设等差数列的公差为
，则有
解方程组得
和公差,即可代入公式求数列
的通项公式及前
项和
．
试题解析：(1)设等比数列的公比为
由，得
解得
3分
∴数列的通项公式
，即 5分
(2)由(1)得
，
，则
，
6分
设等差数列的的公差为，则有
∴
，解得
8分
∴数列的通项公式
9分
∴数列的前项和
10分
12分
考点：1、等差数列、等比数列的定义及通项公式；2、等差数列的前项和.
练习册系列答案
阅读快车系列答案
相关题目
