题目内容
若焦点在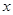 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则
,则 ( )
( )
A. B.
B. C.
C. D.
D.
【答案】
C
【解析】
试题分析:由于焦点在 轴上的椭圆,则可知
轴上的椭圆,则可知 ,由于离心率为
,由于离心率为 ,故得到2=4(2-m),解得m=
,故得到2=4(2-m),解得m= ,故选C.
,故选C.
考点:本题主要考查了椭圆的性质的运用。
点评:解决该试题的关键是理解方程中的,a,b的值,结合离心率的性质得到a,c的比值关系式,进而得到参数m的值。

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则
,则 等于( )
等于( ) B.
B.
 C.
C.
 D.
D.

 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则m的值为( )
,则m的值为( ) C
C
 D
D

 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则m=( )
,则m=( ) B.
B. C.
C. D.
D.
 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点
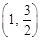 .
. (2,1)的直线
(2,1)的直线 与椭圆
与椭圆 ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 ,由题意得
,由题意得

 ,代入椭圆
,代入椭圆 .
. ,
,
 .解得。
.解得。 .……………………4分
.……………………4分 .
.
 ,
, ,
,
 .
. .
. ,解得
,解得 .
.