题目内容
已知f(x)=3x,并且f(a+2)=18,g(x)=3ax-4x的定义域为区间[-1,1].
(1)求函数g(x)的解析式;
(2)求函数g(x)的值域.
(1)求函数g(x)的解析式;
(2)求函数g(x)的值域.
(1)∵f(a+2)=18,∴3a+2=9•3a=18,即3a=2,∴a=log32,
∴g(x)=3ax-4x=(3a)x-4x=(3log32)x-4x=2x-4x.
(2)∵g(x)=2x-4x=-(2x-
)2+
,
∵-1≤x≤1,
∴
≤2x≤2,
∴设t=2x,则
≤t≤2,
则函数g(x)等价为m(t)=-(t-
)2+
,
∴m(t)单调递减,
∴-2≤m(t)≤
,
即函数g(x)的值域为[-2,
].
∴g(x)=3ax-4x=(3a)x-4x=(3log32)x-4x=2x-4x.
(2)∵g(x)=2x-4x=-(2x-
| 1 |
| 2 |
| 1 |
| 4 |
∵-1≤x≤1,
∴
| 1 |
| 2 |
∴设t=2x,则
| 1 |
| 2 |
则函数g(x)等价为m(t)=-(t-
| 1 |
| 2 |
| 1 |
| 4 |
∴m(t)单调递减,
∴-2≤m(t)≤
| 1 |
| 4 |
即函数g(x)的值域为[-2,
| 1 |
| 4 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
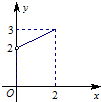
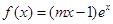 在
在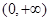 上单调递增,则实数
上单调递增,则实数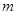 的取值范围是 .
的取值范围是 . 的定义域为
的定义域为
 的定义域为
的定义域为 的定义域为
的定义域为


