题目内容
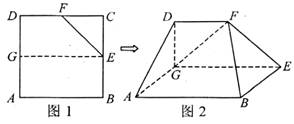
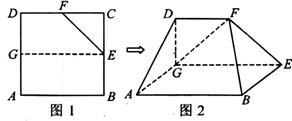
如图所示,平面多边形ABCDP是由梯形ABCD和等边△PAD组成,已知AB//DC ,BD=2AD=4,AB=2DC=![]() ,现将△PAD沿AD折起,使点P的射影
,现将△PAD沿AD折起,使点P的射影![]() 恰好落在直线AD上.
恰好落在直线AD上.
(1)求证:BD⊥平面PAD;
(2)求平面PAD与平面PAB所成的二面角的余弦值。


如图所示,平面多边形ABCDP是由梯形ABCD和等边△PAD组成,已知AB//DC ,BD=2AD=4,AB=2DC=![]() ,现将△PAD沿AD折起,使点P的射影
,现将△PAD沿AD折起,使点P的射影![]() 恰好落在直线AD上.
恰好落在直线AD上.
 (1)求证:BD⊥平面PAD;
(1)求证:BD⊥平面PAD;
(2)求平面PAD与平面PAB所成的二面角的余弦值。
(1)证明:由题意知平面PAD⊥平面ABCD,又BD=2AD=4,AB=![]() 可得AB2=AD2+BD2,则BD⊥AD,又AD为平面PAD与平面ABCD的交线,则BD⊥平面PAD;
可得AB2=AD2+BD2,则BD⊥AD,又AD为平面PAD与平面ABCD的交线,则BD⊥平面PAD;
-----6分
(2)如图建立空间直角坐标,易知A(1,0,0),B(-1,4,0),
P(0,0,![]() ),
),![]() ,
,![]() ,
,
平面PDA的法向量为![]() =(0,1,0),设平面PAB的法向量为
=(0,1,0),设平面PAB的法向量为![]()
由 ,得
,得 ,取
,取![]() 则
则
所以平面PAD与平面PAB所成的二面角的余弦值为![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示,∠ABC=45°,AB=2,AD=1,DC⊥BC,则这块菜地的面积为( )
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示,∠ABC=45°,AB=2,AD=1,DC⊥BC,则这块菜地的面积为( ) 有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示),则这块菜地的面积为
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示),则这块菜地的面积为