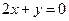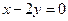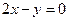题目内容
直线l绕它与x轴的交点顺时针旋转
，得到直线
x+y-
=0，则直线l的直线方程（ ）
| π |
| 3 |
| 3 |
| 3 |
A．x-
| B．
| C．x+
| D．
|
直线直线
x+y-
=0的斜率等于-
，设倾斜角等于θ，即θ=
，
绕它与x轴的交点（
，0）顺时针旋转
，
所得到的直线的倾斜角等于θ-
，故所求直线的斜率为tan（
-
，）=
，
故所求的直线方程为 y-0=
（x-
），即
x-y-3=0，
故选B．
| 3 |
| 3 |
| 3 |
| 2π |
| 3 |
绕它与x轴的交点（
| 3 |
| π |
| 3 |
所得到的直线的倾斜角等于θ-
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| 3 |
故所求的直线方程为 y-0=
| 3 |
| 3 |
| 3 |
故选B．
练习册系列答案
相关题目
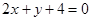与圆C：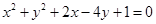
的两个交点，并且面积有最小值，求此圆的方程．
）关于直线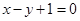
对称，并且圆C与
其中
，当
，
变化时，则满足条件的点
在平面上所组成图形的面积是（ ）
(
所表示的曲线是( )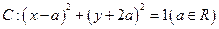
，则下列一定经过圆心的直线方程为
