Question

已知α∈［0,π),试讨论当α的值变化时,方程x²sinα+y²cosα=1表示曲线的形状.

Answer 1

解:(1)当α=0时,方程为y²=1,即y=±1,表示两条平行于x轴的直线.

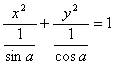(2)当α∈(0,)时,cosα＞sinα＞0,方程化为,表示焦点在x轴上的椭圆.

(3)当时,方程为x²+y²=,表示圆心在原点,半径为的圆.

(4)当时,sinα＞cosα＞0,方程x²sinα+y²cosα=1表示焦点在y轴上的椭圆.

(5)当时,方程化为x²=1,即x=±1,表示两条平行于y轴的直线.

(6)当时, sinα＞0,cosα＜0,方程x²sinα+y²cosα=1表示焦点在x轴上的双曲线.

启示:方程x²sinα+y²cosα=1表示的曲线的形状由sinα和cosα的值确定,sinα和cosα的值又由α的值确定.α在不同范围内取值时,方程x²sinα+y²cosα=1表示的曲线的形状不同.因此,解答本例的关键之处在于对α的分类讨论.