题目内容
已知奇函数f(x)是定义在R上的增函数,a、b∈R,若f(a)+f(b)≥0,求证:a+b≥0.
分析:此题可改为命题:已知奇函数f(x)是定义在R上的增函数,a、b∈R,若f(a)+f(b)≥0,则a+b≥0.
若命题不容易判断时,可对其逆否命题进行判断得到结论.
此命题的逆否命题为:已知奇函数f(x)是定义在R上的增函数,a、b∈R,若a+b<0,则f(a)+f(b)<0.
证明:可证明其逆否命题.假设a+b<0,即a<-b,∵f(x)在R上是增函数,∴f(a)<f(-b).又f(x)为奇函数,∴f(-b)=-f(b).∴f(a)<-f(b),即f(a)+f(b)<0.即原命题的逆否命题为真,∴原命题为真.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 <m<
<m<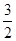 B、
B、 <m<
<m< C、
C、 D、
D、