题目内容
(本小题满分10分)
设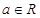 ,函数
,函数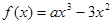 .
.
(Ⅰ) 若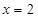 是函数
是函数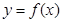 的极值点,求实数
的极值点,求实数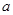 的值;
的值;
(Ⅱ)求函数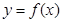 在区间
在区间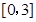 上的最大值和最小值;
上的最大值和最小值;
(Ⅲ)若函数 在
在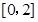 上是单调递减函数,求实数
上是单调递减函数,求实数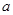 的取值范围.
的取值范围.
【答案】
解:(Ⅰ) 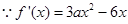 ,
, 是函数
是函数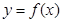 的极值点
的极值点
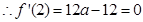
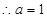
(Ⅱ)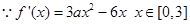 下面分类讨论:
下面分类讨论:
①当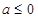 时,因为
时,因为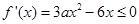 ,易知
,易知 在
在 上是减函数,
上是减函数,
所以 ,
,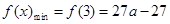 ;
;
②当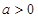 时,因为
时,因为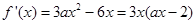 ,
,
令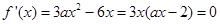 得
得 或
或 ;
;
令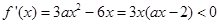 得
得 ;
;
令 得
得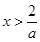 或
或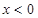 ;
;
若 ,即
,即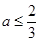 时,
时, 在
在 上是减函数,
上是减函数,
所以 ,
,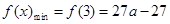 ;
;
若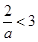 ,即
,即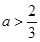 时,易知
时,易知 是
是 在
在 内的极小值点也是最小值点,
内的极小值点也是最小值点,
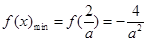 ,
,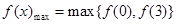
当 时,
时,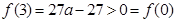 ,
,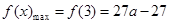 ;
;
当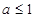 时,
时,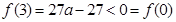 ,
, ;
;
综上所述,当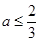 时,
时,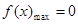 ,
,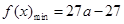 ;
;
当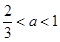 时,
时,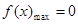 ,
,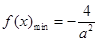 ;
;
当 时,
时,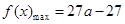 ,
,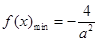 .
.
(Ⅲ) 因为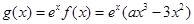 在
在 上是单调递减函数,
上是单调递减函数,
所以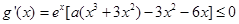 ,
, 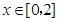
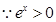
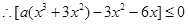
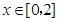
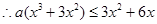
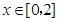
当 时,
时,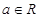 ,都有
,都有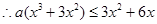 成立;
成立;
当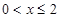 时,
时,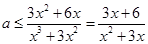 .
.
记 ,
,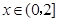
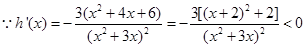
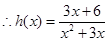 在
在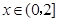 上单调递减,
上单调递减,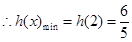

综上所述 的取值范围是
的取值范围是 .
.
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,