题目内容
若函数f（x）在R上可导，且满足f（x）＞xf′（x），则
- A.3f（1）＞f（3）
- B.3f（1）＜f（3）
- C.3f（1）=f（3）
- D.f（1）=f（3）
A
分析：根据条件f（x）＞xf′（x）可构造函数g（x）=
，然后得到函数的单调性，从而得到所求．
解答：设g（x）=，g′（x）=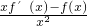
∵f（x）＞xf′（x），
∴g′（x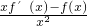）=＜0
即g（x）在（0，+∞）上单调递减函数
∴
即3f（1）＞f（3）
故选A．
点评：本题主要考查了导数除法的运算法则，以及利用构造法是解题的关键，同时考查了运算求解的能力，属于基础题．
分析：根据条件f（x）＞xf′（x）可构造函数g（x）=
，然后得到函数的单调性，从而得到所求．解答：设g（x）=
，g′（x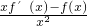）=∵f（x）＞xf′（x），
∴g′（x）=
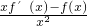＜0即g（x）在（0，+∞）上单调递减函数
∴
即3f（1）＞f（3）故选A．
点评：本题主要考查了导数除法的运算法则，以及利用构造法是解题的关键，同时考查了运算求解的能力，属于基础题．
练习册系列答案
智能训练练测考系列答案
相关题目