题目内容
已知函数
 求函数
求函数 的单调区间.
的单调区间.
【解析】函数 的定义域为
的定义域为 ,
,
令 ,得
,得 ,
,
由于 ,所以
,所以
①当 时,
时, ,此时,
,此时, 在定义域
在定义域 上单调递增,
上单调递增,
②当 时,
时,
令 ,得
,得 ;令
;令 ,得
,得
即 当 时,
时, ,
, 在
在 上单调递增;当
上单调递增;当 时,
时, ,
, 在
在 上单调递减
上单调递减
③当 时,
时,
令 ,得
,得 ;令
;令 ,得
,得
即 当 时,
时, ,
, 在
在 上单调递减;当
上单调递减;当 时,
时, ,
, 在
在 上单调递增
上单调递增
综上所述:当 时,
时, 的递增区间为
的递增区间为 ;当
;当 时,
时, 的递增区间为
的递增区间为 ,递减区间为
,递减区间为 ;当
;当 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 .
.

练习册系列答案
相关题目
 ,求
,求 的最大值
的最大值  .
. 的单调性;(2)求证:对于定义域内的任意一个
的单调性;(2)求证:对于定义域内的任意一个 ,都有
,都有 .
. 在
在 处的切线方程为( )
处的切线方程为( ) B.
B. C.
C. D.
D. 
 ;
; ,
, ,其中
,其中 ,讨函数
,讨函数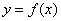 的图象如图1所示,那么导函数
的图象如图1所示,那么导函数 的图象可能是 ( )
的图象可能是 ( )
 满足
满足 ,求
,求 .
. …
… .
.