题目内容
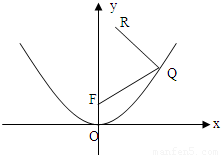
如图所示,F是抛物线x2=2py(p>0)的焦点,点R(1,4)为抛物线内一定点,点Q为抛物线上一动点,|QR|+|QF|的最小值为5.(1)求抛物线方程;
(2)已知过点P(0,-1)的直线l与抛物线x2=2py(p>0)相交于A(x1,y1)、B(x2,y2)两点,l1、l2分别是该抛物线在A、B两点处的切线,M、N分别是l1、l2与直线y=-1的交点.求直线l的斜率的取值范围并证明|PM|=|PN|.
【答案】分析:(1)利用抛物线的定义,结合|QR|+|QF|的最小值为5,建立方程,即可求得抛物线的方程;
(2)设直线l的方程与抛物线方程联立,确定k的范围,求出抛物线在A、B处的切线方程,令y=-1,可得M、N的横坐标,利用韦达定理,可得横坐标互为相反数,从而可得结论.
解答:(1)解:设抛物线的准线为QQ'⊥l于Q',过Q作QQ'⊥l于Q',过R作RR'⊥l于R',由抛物线定义知|QF|=|QQ'|,…(1分)
∴|QR|+|QF|=|QR|+|QQ'|≥|RR'|(折线段大于垂线段),当且仅当R、Q、R'三点共线取等号.…(3分)
由题意知|RR′|=5,
∴ ,
,
∴p=2,故抛物线的方程为:x2=4y…(5分)
(2)证明:由已知条件可知直线l的斜率存在且不为0,设直线l:y=kx-1,…(6分)
则 ,∴x2-4ky+4=0,…①…(7分)
,∴x2-4ky+4=0,…①…(7分)
依题意,有△=16k2-16>0,∴k<-1或k>1;…(8分)
由x2=4y,∴ ,∴
,∴ ,…(9分)
,…(9分)
所以抛物线在A处的切线l1的方程为: ,即
,即 .…(10分)
.…(10分)
令y=-1,得 .…(11分)
.…(11分)
同理,得 .…(12分)
.…(12分)
注意到x1、x2是方程①的两个实根,故x1x2=4,即 ,…(13分)
,…(13分)
从而有 ,
,
因此,|PM|=|PN|.…(14分)
点评:本题考查抛物线的定义,考查直线与抛物线的位置关系,考查韦达定理的运用,属于中档题.
(2)设直线l的方程与抛物线方程联立,确定k的范围,求出抛物线在A、B处的切线方程,令y=-1,可得M、N的横坐标,利用韦达定理,可得横坐标互为相反数,从而可得结论.
解答:(1)解:设抛物线的准线为QQ'⊥l于Q',过Q作QQ'⊥l于Q',过R作RR'⊥l于R',由抛物线定义知|QF|=|QQ'|,…(1分)
∴|QR|+|QF|=|QR|+|QQ'|≥|RR'|(折线段大于垂线段),当且仅当R、Q、R'三点共线取等号.…(3分)
由题意知|RR′|=5,
∴
 ,
,∴p=2,故抛物线的方程为:x2=4y…(5分)
(2)证明:由已知条件可知直线l的斜率存在且不为0,设直线l:y=kx-1,…(6分)
则
 ,∴x2-4ky+4=0,…①…(7分)
,∴x2-4ky+4=0,…①…(7分)依题意,有△=16k2-16>0,∴k<-1或k>1;…(8分)
由x2=4y,∴
 ,∴
,∴ ,…(9分)
,…(9分)所以抛物线在A处的切线l1的方程为:
 ,即
,即 .…(10分)
.…(10分)令y=-1,得
 .…(11分)
.…(11分) 同理,得
 .…(12分)
.…(12分)注意到x1、x2是方程①的两个实根,故x1x2=4,即
 ,…(13分)
,…(13分)从而有
 ,
,因此,|PM|=|PN|.…(14分)
点评:本题考查抛物线的定义,考查直线与抛物线的位置关系,考查韦达定理的运用,属于中档题.

练习册系列答案
相关题目
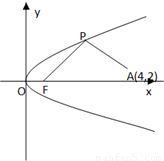
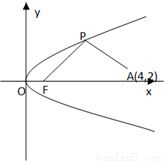
 如图所示,F是抛物线y2=2px(p>0)的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点,|PA|+|PF|的最小值为8.
如图所示,F是抛物线y2=2px(p>0)的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点,|PA|+|PF|的最小值为8.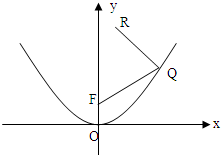 如图所示,F是抛物线x2=2py(p>0)的焦点,点R(1,4)为抛物线内一定点,点Q为抛物线上一动点,|QR|+|QF|的最小值为5.
如图所示,F是抛物线x2=2py(p>0)的焦点,点R(1,4)为抛物线内一定点,点Q为抛物线上一动点,|QR|+|QF|的最小值为5.