题目内容
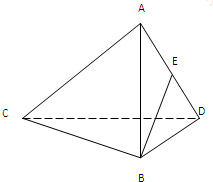 如图,四面体ABCD中,E为AD中点,若AC=CD=DA=8,AB=BD=5,BC=7,求BE与CD所成角的余弦值.
如图,四面体ABCD中,E为AD中点,若AC=CD=DA=8,AB=BD=5,BC=7,求BE与CD所成角的余弦值.分析:取AC中点F,连结BF、EF,由三角形中位线定理证出∠BEF(或补角)就是BE与CD所成角.利用解三角形的知识,算出△BEF中的各边长,利用余弦定理加以计算,即可得到BE与CD所成角的余弦值.
解答:解: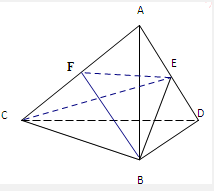 取AC中点F,连结BF、EF
取AC中点F,连结BF、EF
∵EF为△ACD的中位线,
∴EF
CD,可得∠BEF(或补角)就是BE与CD所成角
∵△ABC中,AB=5,BC=7,AC=8.
∴中线BF满足4BF2+AC2=2(BC2+AB2),即4BF2+64=2(49+25),
解之得BF=
∵△ABD中,AB=BD=5,DA=8
∴BE=
=
=3
在△BEF中,cos∠BEF=
=
即BE与CD所成角的余弦值等于
.
 取AC中点F,连结BF、EF
取AC中点F,连结BF、EF∵EF为△ACD的中位线,
∴EF
| ∥ |
. |
| 1 |
| 2 |
∵△ABC中,AB=5,BC=7,AC=8.
∴中线BF满足4BF2+AC2=2(BC2+AB2),即4BF2+64=2(49+25),
解之得BF=
| 21 |
∵△ABD中,AB=BD=5,DA=8
∴BE=
| AB2-AE2 |
| 25-16 |
在△BEF中,cos∠BEF=
| BE2+EF2-BF2 |
| 2•BE•EF |
| 1 |
| 6 |
即BE与CD所成角的余弦值等于
| 1 |
| 6 |
点评:本题在特殊三棱锥中求异面直线所成角的余弦.着重考查了三角形中位定理、解三角形和异面直线所成角的定义及其求法等知识,属于中档题.

练习册系列答案
相关题目
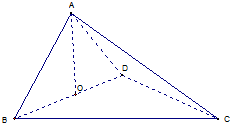 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形, 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD= 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.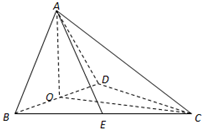 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.