题目内容
(本小题满分13分)在△ABC中,满足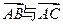 的夹角为
的夹角为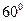 ,M是AB的中点
,M是AB的中点
(1)若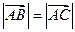 ,求向量
,求向量 的夹角的余弦值
的夹角的余弦值
(2)若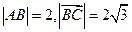 ,在AC上确定一点D的位置,使得
,在AC上确定一点D的位置,使得 达到最小,并求出最小值。
达到最小,并求出最小值。
(1)设
(2)因为 ,由余弦定理可得:
,由余弦定理可得:
M是AB的中点,所以AM=1,因为D是AC上一点,设 ,所以
,所以
=
所以当 时,即D距A点
时,即D距A点 处
处 取到最小,最小值为
取到最小,最小值为
解析

练习册系列答案
相关题目
平面向量 与
与 的夹角为60°,
的夹角为60°, ,
, ,则
,则 ( ).
( ).
| A.9 | B. | C.3 | D.7 |
已知向量 满足
满足 ,则向量
,则向量 夹角的余弦值为 ( )
夹角的余弦值为 ( )
A.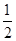 | B. | C. | D. |
下列向量中,与向量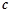
 不共线的一个向量
不共线的一个向量
 ( )
( )
A. | B. | C. | D. |
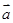 =(-1,1),
=(-1,1), =(x,3),
=(x,3), =(5,y),
=(5,y), =(8,6),且
=(8,6),且 ,函数
,函数
 的单调递减区间.
的单调递减区间. 的图象向左平移
的图象向左平移 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数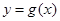 的图象.求
的图象.求 在
在
 上的值域.
上的值域. ,
, ,
, ,求实数
,求实数 的值;
的值; ,求实数
,求实数 =λ
=λ +μ
+μ ,则λ+μ=( )
,则λ+μ=( ) B.
B. C.
C. D.
D.