题目内容
已知抛物线C的顶点在原点, 焦点为F(2, 0).
(1)求抛物线C的方程;
(2)过![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,又
两点,又![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() ,
,
求![]() 的取值范围.
的取值范围.
解:(1) 解:![]() ,
,![]() 得
得![]() ,
,
则![]() ………3分
………3分
![]()
![]()
![]()
![]() ; 递减区间为
; 递减区间为![]() ……7分
……7分
(2)由(1)得
| x | -1 |
|
|
|
|
| 2 |
|
| + | 0 | - | 0 | + | ||
|
| -20 | 增 |
| 减 |
| 增 | 4 |
所以当![]() 时,
时,![]() , ………9分
, ………9分
假设对任意的![]() 都存在
都存在![]() 使得
使得![]() 成立,
成立,
设![]() 的最大值为T,最小值为t,则
的最大值为T,最小值为t,则![]() ………11分
………11分
又![]() ,所以当
,所以当![]() 时,
时,
![]() 且
且![]() ,所以
,所以![]() .………15分22. 解: .解:(1)设抛物线方程为
.………15分22. 解: .解:(1)设抛物线方程为![]() ,则
,则![]() ,
,![]()
所以,抛物线的方程是![]() . …………………4分
. …………………4分
(2)直线![]() 的方程是
的方程是![]() ,联立
,联立![]() 消去
消去![]() 得
得![]() ,…6分
,…6分
显然![]() ,由
,由![]() ,得
,得![]() . ……………8分
. ……………8分
由韦达定理得,![]() ,
,
所以![]() ,则
,则![]() 中点
中点![]() 坐标是
坐标是![]() ,……10分
,……10分
由 ![]() 可得
可得 ![]() ,
,
所以,![]() ,令
,令![]() ,则
,则![]() ,其中
,其中![]() ,…………12分
,…………12分
因为![]() ,所以函数
,所以函数![]() 是在
是在![]() 上增函数.
上增函数.
所以,![]() 的取值范围是
的取值范围是![]() . ……………………15分
. ……………………15分

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
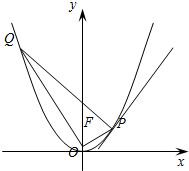 已知抛物线C的顶点在原点,焦点为F(0,1).
已知抛物线C的顶点在原点,焦点为F(0,1).