题目内容
设函数 ,曲线
,曲线 在点(1,
在点(1, 处的切线为
处的切线为 . (Ⅰ)求
. (Ⅰ)求 ; (Ⅱ)证明:
; (Ⅱ)证明: .
.
 设函数()
设函数() ,则
,则 ,所以当
,所以当 ()时,
()时, (),当
(),当 ()时,
()时, (),故
(),故 ()在()
()在() 单调递减,在()
单调递减,在() 单调递增,从而()
单调递增,从而() 在
在 ()¥的最小值为(
()¥的最小值为( . ………10分
. ………10分
设函数() ,则
,则 ,所以当
,所以当 ()时,
()时, (),当
(),当 ()时,
()时, (),故
(),故 ()在()
()在() 单调递增,在()
单调递增,在() 单调递减,从而()
单调递减,从而() 在
在 ()¥的最大值为(
()¥的最大值为( .
.
综上:当 时,
时, ,即
,即 .
.

练习册系列答案
相关题目
 ,
, ,若
,若 与
与
 平
平 行,则
行,则 等于
等于 B.
B. C.
C. D.
D.
 的展开式中的常数项是 。
的展开式中的常数项是 。 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的取值范围是( )
的取值范围是( )  B.
B.  C.
C. D.
D. 
 ,则它的极坐标是( )
,则它的极坐标是( ) B.
B. C.
C. D.
D.
 ,若
,若 ,则
,则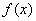 的图象向右平移
的图象向右平移 个单位得到的函数解析式为
个单位得到的函数解析式为 B.
B.