题目内容
证明A(2,2)、B(5,3)、C(3,-1)、D(6,0)四点共圆,并求出此圆的圆心和半径.
思路分析:首先由不共线三点确定一个圆,然后再证第四个点在圆上,用待定系数法.
解法一:设所共圆的方程为x2+y2+Dx+Ey+F=0.
将A、B、D三点坐标代入得
故过A、B、D三点的圆的方程为x2+y2-8x-2y+12=0.
把点C(3,-1)代入方程的左边=9+1-24+2+12=0.
∴点C在该圆上.∵![]() =4,
=4,![]() =1,
=1,
∴圆心为(4,1),r=![]()
综上,可得四点共圆于圆心为(4,1),半径为![]() 的圆,
的圆,
其方程为x2+y2-8x-2y+12=0.
解法二:∵AB边的中点为(![]() ),斜率为kAB=
),斜率为kAB=![]() .
.
∴AB边的垂直平分线的方程为y-![]() =-3(x-
=-3(x-![]() ),
),
即3x+y-13=0.①∵BC的中点为(4,1),kBC=![]() =2,
=2,
∴BC边的垂直平分线的方程为y-1=-![]() (x-4),
(x-4),
即x+2y-6=0.②,解①②组成的方程组得![]()
∴圆心为(4,1),半径r=![]() .
.
∴所求圆的方程为(x-4)2+(y-1)2=5.
绿色通道:圆的标准方程中有三个未知量a,b,r;圆的一般方程有三个未知量D,E,F.故确定一个圆需要三个独立的条件,一般利用待定系数法确定.这需要把题目中的已知条件一一转化为关于未知量的方程,利用方程组获得a,b,r或D,E,F的值,进而确定圆的方程.其基本步骤为:(1)根据题意,设所求的圆的标准方程为(x-a)2+(y-b)2=r2或设方程为x2+y2+Dx+Ey+F=0;(2)根据已知条件,建立关于a、b、r或D,E,F的方程组;(3)解方程组,求出a、b、r或D,E,F的值,并把它们代入所设的方程中去,就得到所求圆的方程.不过有时利用圆的几何性质解题,会有更简捷的解题途径.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
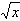 ,g(x)=alnx,a∈R。
,g(x)=alnx,a∈R。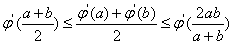 。
。