Question

（2009•台州二模）函数y=f（x）的图象是圆心在原点的单位圆的两段圆弧（如图），则不等式f（x）＜f（-x）+2x的解集为

(-

2

2

，0)∪(

2

2

，1]

．

Answer 1

分析：根据图象得知是奇函数，从而将“不等式f（x）＜f（-x）+2x”转化为“f（x）＜x”，再令y=f（x），y=x，利用图象求解．

解答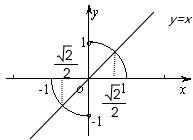：解：由图象可知，函数是奇函数
∴不等式f（x）＜f（-x）+2x可转化为：f（x）＜x，
令y=f（x），y=x，如图所示
∴不等式f（x）＜f（-x）+2x的解集为(-

2

2

，0)∪(

2

2

，1]
故答案为：(-

2

2

，0)∪(

2

2

，1]

点评：本题考查利用函数图象的相对位置关系来解不等式，转化为特定的基本函数，能画其图象是解题的关键．