题目内容

在平面直角坐标系xOy中，已知圆心在第二象限、半径为2的圆C与直线y＝x相切于坐标原点O.椭圆＋＝1与圆C的一个交点到椭圆两焦点的距离之和为10.

(1)求圆C的方程．

(2)试探究圆C上是否存在异于原点的点Q，使Q到椭圆右焦点F的距离等于线段OF的长．若存在，请求出点Q的坐标；若不存在，请说明理由．

解：（1）设圆心坐标为(m,n),则m<0,n>0,

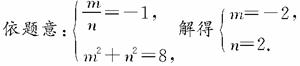
所以圆C的方程为(x+2)2+(y-2)2=8.

因为圆与椭圆的交点在椭圆上，则2a=10,a=5.

所以椭圆的方程为=1.

(2)由椭圆=1,所以F（4，0），

若存在，则F在OQ的中垂线上，

又O、Q在圆C上，所以O、Q关于直线CF对称.

直线CF的方程为y-2=- (x+2),即x+3y-4=0,

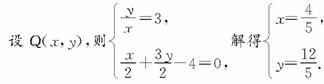
所以存在，Q的坐标为.

练习册系列答案
相关题目
在平面直角坐标系xoy中，已知圆心在直线y=x+4上，半径为2
2
的圆C经过坐标原点O，椭圆
x2
a2
+
y2
9
=1(a＞0)与圆C的一个交点到椭圆两焦点的距离之和为10．
（1）求圆C的方程；
（2）若F为椭圆的右焦点，点P在圆C上，且满足PF=4，求点P的坐标．
如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．若点A的横坐标是
3
5
，点B的纵坐标是
12
13
，则sin（α+β）的值是
16
65
16
65
．
在平面直角坐标系xOy中，若焦点在x轴的椭圆
x2
m
+
y2
3
=1的离心率为
1
2
，则m的值为
4
4
．
（2013•泰州三模）选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，已知A（0，1），B（0，-1），C（t，0），D(
3t
，0)，其中t≠0．设直线AC与BD的交点为P，求动点P的轨迹的参数方程（以t为参数）及普通方程．
（2013•东莞一模）在平面直角坐标系xOy中，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左焦点为F1（-1，0），且椭圆C的离心率e=
1
2
．
（1）求椭圆C的方程；
（2）设椭圆C的上下顶点分别为A1，A2，Q是椭圆C上异于A1，A2的任一点，直线QA1，QA2分别交x轴于点S，T，证明：|OS|•|OT|为定值，并求出该定值；
（3）在椭圆C上，是否存在点M（m，n），使得直线l：mx+ny=2与圆O：x2+y2=
16
7
相交于不同的两点A、B，且△OAB的面积最大？若存在，求出点M的坐标及对应的△OAB的面积；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网