题目内容
如图，O为正方体AC1的底面ABCD的中心，异面直线B1O与A1C1所成角的大小为 ．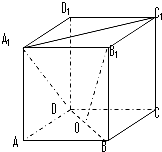
考点：异面直线及其所成的角
专题：空间角
分析：首先，连结B1D1，然后，证明B1D1⊥平面BB1D1D即可．
解答：
解：连结B1D1，
∴A1C1⊥B1D1，
∵A1C1⊥DD1，
∴B1D1⊥平面BB1D1D，
∵B1O?平面BB1D1D，
∴异面直线B1O与A1C1所成角的大小为90°．
故答案为：90°．
∴A1C1⊥B1D1，
∵A1C1⊥DD1，
∴B1D1⊥平面BB1D1D，
∵B1O?平面BB1D1D，
∴异面直线B1O与A1C1所成角的大小为90°．
故答案为：90°．
点评：本题重点考查了直线与直线垂直、直线与平面垂直、异面直线所成的角等知识，属于中档题．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
已知sin（3π+α）=lg
，则tan（π+α）的值是（ ）
| 1 | |||
|
A、-
| ||||
B、
| ||||
C、±
| ||||
D、
|
已知函数y=f（x）是定义域为R的偶函数．当x≥0时，f（x）=
，若关于x的方程[f（x）]2+af（x）+b=0，a，b∈R有且仅有6个不同实数根，则实数a的取值范围是（ ）
|
| A、（-5，-3）∪（-1，0） | ||||
B、(-5，-2)∪(-
| ||||
C、(-5，-
| ||||
D、（-
|
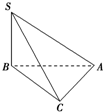三棱锥S-ABC中，∠SBA=∠SCA=90°，△ABC是斜边AB=a的等腰直角三角形，则以下结论中：