题目内容
已知函数![]() ,在点
,在点![]() 处的切线与直线
处的切线与直线![]() 平行。
平行。
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 在
在![]() 上的最小值。
上的最小值。
解:(1)因为函数![]() ,
,
所以定义域为![]() ,
,![]() 。
。
因为在点![]() 处的切线与直线
处的切线与直线![]() 平行,
平行,
所以![]() ,即
,即![]() 。
。
所以![]() 。所以
。所以![]() 。
。
(2)由(Ⅰ)![]() ,令
,令![]() ,得
,得![]() 。
。
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增。
上单调递增。
所以①若![]() 时,函数
时,函数![]() 的最小值是
的最小值是![]()
![]() ;
;
②若![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,所以函数
上单调递增,所以函数![]() 的最小值是
的最小值是![]() 。
。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 (
( ).
).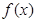 的单调区间;
的单调区间; 的图象为曲线
的图象为曲线 .设点
.设点 ,
, 是曲线
是曲线 ,使得:①
,使得:① ;②曲线
;②曲线 处的切线平行
处的切线平行 ,则称函数
,则称函数 存在“中值相依切线”.试问:函数
存在“中值相依切线”.试问:函数