题目内容
设数列{an}的前n项和为Sn,对任意的正整数n,都有an=3Sn+1成立.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记 ,求数列{bn}的前n项和为Tn.
,求数列{bn}的前n项和为Tn.
解:(1)当n=1时,a1=3S1+1,∴ .
.
又∵an=3Sn+1,an+1=3Sn+1+1,
∴ ,∴
,∴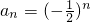 .
.
(2) ,
,
∴ .…①
.…①
故 .…②
.…②
①-②得: ,
,
∴ =
=
= .
.
分析:(1)当n=1时,由a1=3S1+1求出 ,又an=3Sn+1,an+1=3Sn+1+1,相减可得
,又an=3Sn+1,an+1=3Sn+1+1,相减可得 ,从而求得数列{an}的通项公式.
,从而求得数列{an}的通项公式.
(2)先依据题意求出 ,再利用错位相减法求数列的前n项和.
,再利用错位相减法求数列的前n项和.
点评:本题主要考查数列的前n项和与第n项之间的关系,用错位相减法求数列的前n项和,属于中档题.
 .
.又∵an=3Sn+1,an+1=3Sn+1+1,
∴
 ,∴
,∴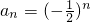 .
.(2)
 ,
,∴
 .…①
.…①故
 .…②
.…②①-②得:
 ,
,∴
 =
=
=
 .
.分析:(1)当n=1时,由a1=3S1+1求出
 ,又an=3Sn+1,an+1=3Sn+1+1,相减可得
,又an=3Sn+1,an+1=3Sn+1+1,相减可得 ,从而求得数列{an}的通项公式.
,从而求得数列{an}的通项公式.(2)先依据题意求出
 ,再利用错位相减法求数列的前n项和.
,再利用错位相减法求数列的前n项和.点评:本题主要考查数列的前n项和与第n项之间的关系,用错位相减法求数列的前n项和,属于中档题.

练习册系列答案
相关题目