题目内容
(提示:1、12、13、14班同学请完成试题(B),其他班级同学任选试题(A)或(B)作答)(A) 已知点A(2,3),B(5,4),C(7,10)及
| AP |
| AB |
| AC |
(1)t为何值时,P在第三象限?
(2)是否存在D点使得四边形ABCD为平行四边形,若存在,求出D点坐标.
(B) 已知平行四边形ABCD,对角线AC与BD交于点E,
| AN |
| 1 |
| 2 |
| ND |
(1)若
| AM |
| AE |
(2)若B(0,0),C(1,0),D(2,1),求M的坐标.
分析:(A)(1)解出P的坐标,令其横纵坐标小于0,即可解出参数t的取值范围.
(2)设出D的坐标,利用向量的相等建立方程求出其坐标,若能求出,则说明存在,否则说明不存在.
(B)(1)选定基向量,利用三角形法则将两个向量用基向量表示出来即可得出参数的值;
(2)由向量的坐标运算规则直接求出M的坐标.
(2)设出D的坐标,利用向量的相等建立方程求出其坐标,若能求出,则说明存在,否则说明不存在.
(B)(1)选定基向量,利用三角形法则将两个向量用基向量表示出来即可得出参数的值;
(2)由向量的坐标运算规则直接求出M的坐标.
解答:解:(A)(1)∵A(2,3),B(5,4),C(7,10)及
=
+t
,
∴
=
+t
=(3,1)+t(5,7)=(3+5t,1+7t)
∴P(5+5t,4+7t)
又P在第三象限,故有
解得t<-1
(2)存在D(x,y)使得四边形ABCD为平行四边形,因为
∵四边形ABCD为平行四边形,令AC,与BD的交点为E,则E是对角线的中点,可求得E(
,
),
∴
故D(4,9)
(B)(1)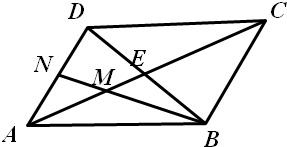 如图,以
如图,以
,
为基向量,则
=
(
+
) ①
=
+
=
+α
=
+α(
-
)=
+α(
-
)=α
+
(1-α)
又
=β
=β(
+
)
故有
解得α=β=
,即
=
=
(
+
) ②
由①②知,M是A,E的中点故λ=
,
(2)∵B(0,0),C(1,0),D(2,1),
∴
=(-1,0),
=(1,1)
∴
=(0,1),
由上,
=
,即,
=-
=(0,-
)
| AP |
| AB |
| AC |
∴
| AP |
| AB |
| AC |
∴P(5+5t,4+7t)
又P在第三象限,故有
|
(2)存在D(x,y)使得四边形ABCD为平行四边形,因为
∵四边形ABCD为平行四边形,令AC,与BD的交点为E,则E是对角线的中点,可求得E(
| 9 |
| 2 |
| 13 |
| 2 |
∴
|
(B)(1)
 如图,以
如图,以| AB |
| AD |
| AE |
| 1 |
| 2 |
| AB |
| AD |
| AM |
| AN |
| NM |
| 1 |
| 3 |
| AD |
| NB |
| 1 |
| 3 |
| AD |
| AB |
| AN |
| 1 |
| 3 |
| AD |
| AB |
| 1 |
| 3 |
| AD |
| AB |
| 1 |
| 3 |
| AD |
又
| AM |
| AC |
| AB |
| AD |
故有
|
| 1 |
| 4 |
| AM |
| 1 |
| 4 |
| AC |
| 1 |
| 4 |
| AB |
| AD |
由①②知,M是A,E的中点故λ=
| 1 |
| 2 |
(2)∵B(0,0),C(1,0),D(2,1),
∴
| CB |
| CD |
∴
| CA |
由上,
| AM |
| 1 |
| 4 |
| AC |
| AM |
| 3 |
| 4 |
| CA |
| 3 |
| 4 |
点评:本题考查向量的坐标运算,求解本题的关键是掌握住向量的加减法则,本题是一个向量综合题,综合考查了向量的三角形法则,向量的坐标运算,运算量较大,易因马虎导致出错,做题时要严谨.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
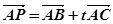 ,试问:
,试问: ,连接BN交AC于M,
,连接BN交AC于M,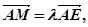 求实数λ.
求实数λ.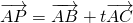 ,试问:
,试问: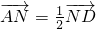 ,连接BN交AC于M,
,连接BN交AC于M,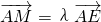 ,求实数λ.
,求实数λ.