题目内容
等比数列{an}的公比q>1,第17项的平方等于第24项,则使a1+a2+…+an> +
+ +…+
+…+ 恒成立的正整数n的最小值为
恒成立的正整数n的最小值为
- A.18
- B.19
- C.20
- D.21
C
分析:由等比数列的性质知:数列{ }是以
}是以 为首项,以
为首项,以 为公比的等比数列,要使不等式成立,则须
为公比的等比数列,要使不等式成立,则须
 ,由等比数列{an}的公比q>1,第17项的平方等于第24项,化简代入,即可求得结论.
,由等比数列{an}的公比q>1,第17项的平方等于第24项,化简代入,即可求得结论.
解答:由题意得:(a1q16)2=a1q23,∴a1q9=1.
由等比数列的性质知:数列{ }是以
}是以 为首项,以
为首项,以 为公比的等比数列,
为公比的等比数列,
要使不等式成立,则须

将 代入上式并整理,得q-18(qn-1)>q(1-
代入上式并整理,得q-18(qn-1)>q(1-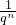 ),
),
∴qn>q19,
∵q>1,∴n>19,故所求正整数n的最小值是20.
故选C.
点评:本题考查等比数列的确定与等比数列的求和,考查等比数列的性质,属于基础题.
分析:由等比数列的性质知:数列{
 }是以
}是以 为首项,以
为首项,以 为公比的等比数列,要使不等式成立,则须
为公比的等比数列,要使不等式成立,则须
 ,由等比数列{an}的公比q>1,第17项的平方等于第24项,化简代入,即可求得结论.
,由等比数列{an}的公比q>1,第17项的平方等于第24项,化简代入,即可求得结论.解答:由题意得:(a1q16)2=a1q23,∴a1q9=1.
由等比数列的性质知:数列{
 }是以
}是以 为首项,以
为首项,以 为公比的等比数列,
为公比的等比数列,要使不等式成立,则须


将
 代入上式并整理,得q-18(qn-1)>q(1-
代入上式并整理,得q-18(qn-1)>q(1-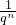 ),
),∴qn>q19,
∵q>1,∴n>19,故所求正整数n的最小值是20.
故选C.
点评:本题考查等比数列的确定与等比数列的求和,考查等比数列的性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的前n项和为Tn,是否存在正整数p,q,使不等式
的前n项和为Tn,是否存在正整数p,q,使不等式 对一切n∈N*都成立?若存在,求出p,q的值;若不存在,说明理由.
对一切n∈N*都成立?若存在,求出p,q的值;若不存在,说明理由.