题目内容

在△ABC中，AB=2，BC=3，∠ABC=60°，AD为BC边上的高，O为AD的中点，若
AO
=λ
AB
+μ
BC
，则λ+μ=
2
3
2
3
．
分析：因为AB=2，BC=3，∠ABC=60°，所以
AB
•
BC
=
|AB|
•
|BC|
cos120°=-3，再根据O为AD的中点，且
AO
=λ
AB
+μ
BC
，可得
AD
=2λ
AB
+2μ
BC
，从而
AD
•
BC
=-6λ+18μ=0，得λ=3μ．接下来利用
BD
=
AD
-
AB
，结合
BD
与
BC
是共线向量，可算得λ=
1
2
，代入上式得μ=
1
6
，最终得到λ+μ的值为
2
3
．
解答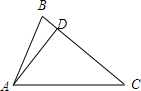：解：∵AB=2，BC=3，∠ABC=60°，
∴
AB
•
BC
=
|AB|
•
|BC|
cos120°=-3
∵O为AD的中点，
AO
=λ
AB
+μ
BC
，
∴
AD
=2
AO
=2λ
AB
+2μ
BC
，
可得
AD
•
BC
=（2λ
AB
+2μ
BC
）•
BC
=2λ
AB
•
BC
+2μ
BC
2=-6λ+18μ
∵AD为BC边上的高，
AD
与
BC
互相垂直
∴
AD
•
BC
=0，即-6λ+18μ=0，得λ=3μ…①
又∵
AD
=2λ
AB
+2μ
BC
，
BD
=
AD
-
AB

∴
BD
=（2λ-1）
AB
+2μ
BC
，
而
BD
与
BC
是共线向量，可得2λ-1=0，所以λ=
1
2
，再代入①，得μ=
1
6

∴λ+μ的值为
2
3

故答案为
2
3
．
点评：本题给出一个特殊的三角形ABC，一条高线AD中点为O，要我们将向量
AO
表示为
AB
、
BC
的线性组合的形式，着重考查了平面向量平行与共线的充要条件及其表示式，属于基础题．
练习册系列答案
相关题目
在△ABC中，AB=AC，D、E分别是AB、AC的中点，则（　　）
在△ABC中，AB=4，AC=2，S△ABC=2
3
．
（1）求△ABC外接圆的面积．
（ 2）求cos（2B+
π
3
）的值．
在△ABC中，AB=a，AC=b，当
a
•
b
＜0时，△ABC为
钝角三角形
钝角三角形
．
在△ABC中，AB=2，BC=3，AC=
7
，则△ABC的面积为
3
3
2
3
3
2
，△ABC的外接圆的面积为
7π
3
7π
3
．
在△ABC中，
AB
=
a
，
AC
=
b
，M为AB的中点，
BN
=
1
3
BC
，则
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网