题目内容
学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且 .
.
(1)求文娱队的队员人数;
(2)写出 的概率分布列并计算
的概率分布列并计算
 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且 .
.(1)求文娱队的队员人数;
(2)写出
 的概率分布列并计算
的概率分布列并计算
(1)2
(2) 的概率分布列为:
的概率分布列为:
∴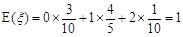 .
.
(2)
 的概率分布列为:
的概率分布列为: | 0 | 1 | 2 |
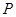 | 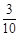 | 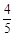 | 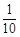 |
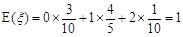 .
.(1)设既会唱歌又会跳舞的有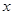 人,则文娱队中共有(
人,则文娱队中共有(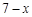 )人,只会一项的人数是(
)人,只会一项的人数是(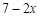 )人,再利用
)人,再利用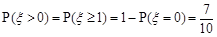 ,∴
,∴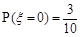 ,即
,即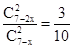 ,可解出x的值.
,可解出x的值.
(2)分别求出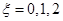 对应的概率,列出分布列,根据期望公式求期望即可.
对应的概率,列出分布列,根据期望公式求期望即可.
设既会唱歌又会跳舞的有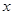 人,
人,
则文娱队中共有(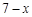 )人,只会一项的人数是(
)人,只会一项的人数是(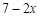 )人.………………2分
)人.………………2分
(1)∵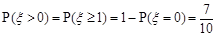 ,∴
,∴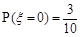 ,即
,即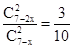 .
.
∴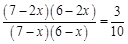 ,解得
,解得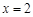 .
.
故文娱队共有5人. ………………………5分
(2)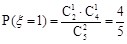 ,
,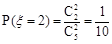 , ………………………7分
, ………………………7分
 的概率分布列为:
的概率分布列为:
∴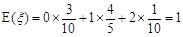 .
.
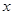 人,则文娱队中共有(
人,则文娱队中共有(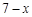 )人,只会一项的人数是(
)人,只会一项的人数是(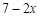 )人,再利用
)人,再利用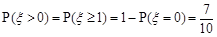 ,∴
,∴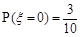 ,即
,即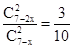 ,可解出x的值.
,可解出x的值.(2)分别求出
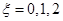 对应的概率,列出分布列,根据期望公式求期望即可.
对应的概率,列出分布列,根据期望公式求期望即可.设既会唱歌又会跳舞的有
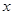 人,
人,则文娱队中共有(
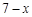 )人,只会一项的人数是(
)人,只会一项的人数是(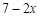 )人.………………2分
)人.………………2分(1)∵
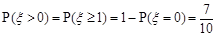 ,∴
,∴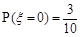 ,即
,即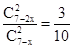 .
.∴
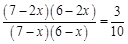 ,解得
,解得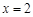 .
.故文娱队共有5人. ………………………5分
(2)
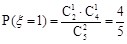 ,
,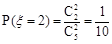 , ………………………7分
, ………………………7分 的概率分布列为:
的概率分布列为: | 0 | 1 | 2 |
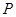 | 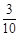 | 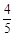 | 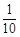 |
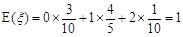 .
.
练习册系列答案
相关题目




 个男生和
个男生和 个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有
个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有 种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有
种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有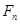 种选法.
种选法. 和
和 ),并用数学归纳法证明.
),并用数学归纳法证明. 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
. 的值;
的值; 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量 .
. 视觉
视觉 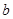

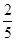 .
. ,求随机变量
,求随机变量 .
. .
.  的概率;
的概率; 的概率分布列如下,且
的概率分布列如下,且 则
则


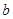
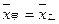 ,方差
,方差 ,则成绩较稳定的同学是 (填“甲”或“乙”)
,则成绩较稳定的同学是 (填“甲”或“乙”)