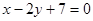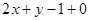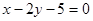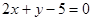题目内容
已知直线 过点
过点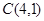 , (1)若直线
, (1)若直线 在两坐标轴上截距相等,求直线
在两坐标轴上截距相等,求直线 的方程。
的方程。
(2)若直线 分别与
分别与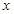 轴、y轴的正半轴相交于
轴、y轴的正半轴相交于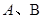 两点,O为坐标原点,记
两点,O为坐标原点,记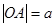
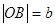 ,求
,求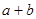 的最小值,并写出此时直线
的最小值,并写出此时直线 的方程。
的方程。
 过点
过点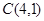 , (1)若直线
, (1)若直线 在两坐标轴上截距相等,求直线
在两坐标轴上截距相等,求直线 的方程。
的方程。(2)若直线
 分别与
分别与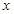 轴、y轴的正半轴相交于
轴、y轴的正半轴相交于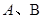 两点,O为坐标原点,记
两点,O为坐标原点,记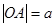
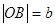 ,求
,求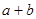 的最小值,并写出此时直线
的最小值,并写出此时直线 的方程。
的方程。(1)  或
或 (2)
(2)
 或
或 (2)
(2)
本题考查的知识点是直线的截距式方程,其中(1)的关键是分析出直线l在两坐标轴上的截距相等包括两种情况,一是过原点,一是斜率为 ,在解答时,易忽略直线l过原点这种情况,而错解为x+y-5=0.
,在解答时,易忽略直线l过原点这种情况,而错解为x+y-5=0.
(1)直线l在两坐标轴上的截距相等包括两种情况,一是过原点,一是斜率为1/4,分别求出两种情况下直线l的方程,进而得到答案;
(2) 设 的方程为:
的方程为: ,
, 直线
直线 过点
过点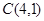 ,
, (1)
(1)
 结合不等式性质得到结论。
结合不等式性质得到结论。
解:(1)若直线 过原点,设其方程为:
过原点,设其方程为: ,又直线
,又直线 过点
过点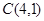 ,则
,则 即
即
若直线 不过原点,设其方程为:
不过原点,设其方程为: ,
, 直线
直线 过点
过点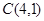 ,
,
直线 的方程为
的方程为 ;综上,
;综上, 的方程为
的方程为 或
或

(2)设 的方程为:
的方程为: ,
, 直线
直线 过点
过点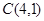 ,
, (1)
(1)
 当且仅当
当且仅当
即 时取等号,将
时取等号,将 与(1)式联立得
与(1)式联立得 ,
, 的方程为
的方程为
综上,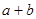 的最小值为9,
的最小值为9, 的方程为
的方程为 ------------10分
------------10分
 ,在解答时,易忽略直线l过原点这种情况,而错解为x+y-5=0.
,在解答时,易忽略直线l过原点这种情况,而错解为x+y-5=0.(1)直线l在两坐标轴上的截距相等包括两种情况,一是过原点,一是斜率为1/4,分别求出两种情况下直线l的方程,进而得到答案;
(2) 设
 的方程为:
的方程为: ,
, 直线
直线 过点
过点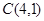 ,
, (1)
(1) 结合不等式性质得到结论。
结合不等式性质得到结论。解:(1)若直线
 过原点,设其方程为:
过原点,设其方程为: ,又直线
,又直线 过点
过点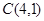 ,则
,则 即
即
若直线
 不过原点,设其方程为:
不过原点,设其方程为: ,
, 直线
直线 过点
过点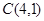 ,
,
直线
 的方程为
的方程为 ;综上,
;综上, 的方程为
的方程为 或
或

(2)设
 的方程为:
的方程为: ,
, 直线
直线 过点
过点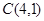 ,
, (1)
(1) 当且仅当
当且仅当
即
 时取等号,将
时取等号,将 与(1)式联立得
与(1)式联立得 ,
, 的方程为
的方程为
综上,
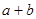 的最小值为9,
的最小值为9, 的方程为
的方程为 ------------10分
------------10分
练习册系列答案
相关题目
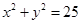 相切的切线方程.
相切的切线方程.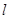 经过点P(5,5)且和圆C:
经过点P(5,5)且和圆C: 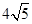 ,求
,求 与直线
与直线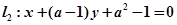 平行,则实数
平行,则实数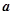 的值是( )
的值是( )



 与直线
与直线 平行,则实数
平行,则实数 .
.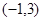 且平行于直线
且平行于直线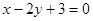 的直线方程为( ).
的直线方程为( ).