题目内容
已知直线y=2x上存在点(x,y)满足约束条件
,则实数m的取值范围是( )
|
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、[2,+∞) |
| D、(-∞,1] |
分析:根据题意,可得当m≤3时不等式组表示的平面区域为非空点集,由此作出不等式组对应的平面区域,得到如图所示的△ABC及其内部.根据直线y=2x上存在一点满足不等式组,可得区域内的点与原点连线倾斜角的最大值大于或等于直线y=2x的倾斜角,结合直线的斜率公式建立关于m的不等式,解之即可得到实数m的取值范围.
解答:解: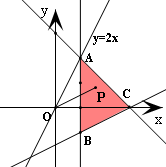 由直线x+y-3=0与x-2y-3=0交于点C(3,0),
由直线x+y-3=0与x-2y-3=0交于点C(3,0),
可得当m≤3时,不等式组
表示的平面区域为非空点集.
此时作出不等式组对应的平面区域,得到如图所示的△ABC及其内部,
其中A(m,3-m),B(m,
(m-3)),C(3,0).
∵直线y=2x上存在点(x,y)满足题中的约束条件,
∴设P(x,y)是区域内一个动点,OP的倾斜角大于或等于直线y=2x的倾斜角,
因此可得
≥2或
<0,
结合m≤3,
解得m≤1.
故选:D
 由直线x+y-3=0与x-2y-3=0交于点C(3,0),
由直线x+y-3=0与x-2y-3=0交于点C(3,0),可得当m≤3时,不等式组
|
此时作出不等式组对应的平面区域,得到如图所示的△ABC及其内部,
其中A(m,3-m),B(m,
| 1 |
| 2 |
∵直线y=2x上存在点(x,y)满足题中的约束条件,
∴设P(x,y)是区域内一个动点,OP的倾斜角大于或等于直线y=2x的倾斜角,
因此可得
| 3-m |
| m |
| 3-m |
| m |
结合m≤3,
解得m≤1.
故选:D
点评:本题已知二元一次不等式组表示的平面区域,在满足给定条件的情况下求参数m的范围.着重考查了直线的斜率公式、二次一次不等式组表示的平面区域和简单的线性规划等知识,属于中档题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点
 .
. (2,1)的直线
(2,1)的直线 与椭圆
与椭圆 ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 ,由题意得
,由题意得

 ,代入椭圆
,代入椭圆 .
. ,
,
 .解得。
.解得。 .……………………4分
.……………………4分 .
.
 ,
, ,
,
 .
. .
. ,解得
,解得 .
.