题目内容
设a，b是正实数，以下不等式：①a+
≥2；②
≥a+b；③
≥
；④a＜|a-b|+b，
其中恒成立的有（ ）
| 1 |
| b |
| 2(a2+b2) |
| ab |
| 2ab |
| a+b |
其中恒成立的有（ ）
| A、①② | B、②③ | C、③④ | D、②④ |
分析：①a，b是正实数，求a+
的最小值，由于不知道ab是否为定值，特殊值法；②分析法证明，两边平方；③根据基本不等式a+b≥2
，取倒数，根据不等式的基本性质可证；④取特殊值，a=3，b=1可知结论不成立．
| 1 |
| b |
| ab |
解答：解：①∵a，b是正实数，而ab不一定是定值，故a+
≥2不一定成立，如a=
，b=1，a+
=
＜2．
②∵a，b是正实数
∴（a+b）2=a2+b2+2ab≤2（a+b）2
∴
≥a+b
③a，b是正实数，a+b≥2
，
∴
≤
，两边同时乘以2ab得
≥
④令a=3，b=1，则|a-b|+b=3=a，故④不成立．
故选B．
| 1 |
| b |
| 1 |
| 2 |
| 1 |
| b |
| 3 |
| 2 |
②∵a，b是正实数
∴（a+b）2=a2+b2+2ab≤2（a+b）2
∴
| 2(a2+b2) |
③a，b是正实数，a+b≥2
| ab |
∴
| 1 |
| a+b |
| 1 | ||
2
|
| ab |
| 2ab |
| a+b |
④令a=3，b=1，则|a-b|+b=3=a，故④不成立．
故选B．
点评：应用基本不等式证明不等式或求最值，应注意正、定、等，要说明一个命题是假命题，只要举一个反例即可，属基础题．
练习册系列答案
相关题目
（选做题）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，若多做，则按作答的前两题评分，解答时应写出文字说明、证明过程或演算步骤．
，
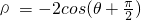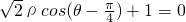，则曲线C1上的点与曲线C2上的点的最远距离为________．
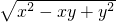，b=p
，c=x+y，若对任意的正实数x，y，都存在以a，b，c为三边长的三角形，则实数p的取值范围是________．
（t为参数），求直线l被曲线C截得的线段长度．
．
（t为参数），求直线l被曲线C截得的线段长度．
．
，
，则曲线C1上的点与曲线C2上的点的最远距离为 ．
，b=p
，c=x+y，若对任意的正实数x，y，都存在以a，b，c为三边长的三角形，则实数p的取值范围是 ．