题目内容
已知-1<a+b<3,2<a-b<4,则2a+3b的范围是( )
A.(-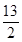 , ,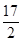 ) ) | B.(-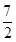 , , ) ) |
C.(-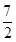 , ,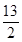 ) ) | D.(-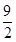 , ,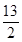 ) ) |
D
解析试题分析:由题意将2a+3b用(a+b)和(a-b)分别表示出来,然后根据-1<a+b<3且2<a-b<4,求出2a+3b的取值范围.
设2a+3b=x(a+b)+y(a-b),则可知 ,解得
,解得
所以- <
<  (a+b)<
(a+b)< ,-
,- <
<  (a-b)<
(a-b)< ,两式相加可知2a+3b的范围是(-
,两式相加可知2a+3b的范围是(-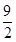 ,
,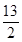 ),选D.
),选D.
考点:本题主要考查了不等关系与不等式之间的关系.
点评:本题用的方法很重要,不要把a,b的范围分别求出来,那样就放大了2a+3b的范围,这是一个易错点.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
若 ,
, ,则
,则 与
与 的大小关系为 ( )
的大小关系为 ( )
A. | B. | C. | D.随x值变化而变化 |
已知 ,
, ,则下列不等式中恒成立的是( )
,则下列不等式中恒成立的是( )
A. | B. | C. | D. |
下列不等式正确的是( )
A. | B. |
C. | D. |
若 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. | B. | C. | D. |
若 ,则下列不等式不一定成立的是( )
,则下列不等式不一定成立的是( )
A. | B. |
C. | D. |
 ,
, ,
, ,则( )
,则( )
A. | B. | C. | D. |
 是定义域为
是定义域为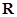 的可导函数,且对任意实数
的可导函数,且对任意实数 都有
都有 成立.若当
成立.若当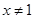 时,不等式
时,不等式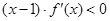 成立,设
成立,设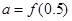 ,
,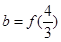 ,
, ,则
,则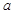 ,
,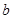 ,
, 的大小关系是( )
的大小关系是( )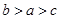
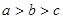
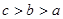
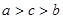
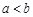 ,则
,则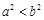 ;
;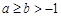 ,则
,则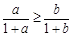 ;
;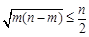 ;
; 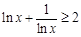 .
.