题目内容
已知两定点F1(-(1)求曲线C的方程;
(2)若曲线C上存在一点D,使![]() +
+![]() =m
=m![]() ,求m的值及点D的坐标.
,求m的值及点D的坐标.
解:(1)由双曲线的定义可知曲线C是以F1(-![]() ,0),F2(
,0),F2(![]() ,0)为焦点的双曲线的左半支.
,0)为焦点的双曲线的左半支.
且c=![]() ,2a=2,a=1,故b=1,所以轨迹C的方程是x2-y2=1(x<0).
,2a=2,a=1,故b=1,所以轨迹C的方程是x2-y2=1(x<0).
(2)设A(x1,y1),B(x2,y2),由题意得方程组 消去y得(1-k2)x2+4kx-5=0.
消去y得(1-k2)x2+4kx-5=0.
又已知直线与曲线C交于A、B两点,
故有 解得-
解得-![]() <k<-1.
<k<-1.
∵|AB|=![]() |x2-x1|=
|x2-x1|=![]() ·
·![]() =2
=2 =
=![]() ,
,
∴![]() =
=![]() .设t=k2,得7t2-23t-20=0,(t-4)(7t+5)=0.∴t=4,t=
.设t=k2,得7t2-23t-20=0,(t-4)(7t+5)=0.∴t=4,t=![]() (舍).
(舍).
又由k2=4,舍去k=2,得k=-2,于是直线AB的方程为y=-2x-2,即2x+y+2=0.
由 解得
解得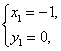

不妨设![]() =(-1,0),
=(-1,0),![]() =(
=(![]() ,
,![]() ),由
),由![]() +
+![]() =m
=m![]() ,故有
,故有![]() =(
=(![]() ,
,![]() ).
).
将D点坐标代入曲线C的方程,得![]() =1.解得m=±
=1.解得m=±![]() ,但当m=
,但当m=![]() 时,
时,
点D在双曲线右支上,不合题意,∴m=![]() .
.
∴点D的坐标为(![]() ,
,![]() ).
).

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目