题目内容
如图,四棱锥P—ABCD的底面是矩形,PA⊥底面ABCD于A,E、F分别是AB、PD之中点.
(1)求证:AF∥平面PCE;
(2)若二面角PCDB为45°,求证:平面PCE⊥平面PCD;
(3)在(2)的条件下,若AD=2,CD=
,求F到平面PCE的距离
(1)证明：取PC的中点M,连结EM、FM,则FM 
CD 
AE
AEMF是平
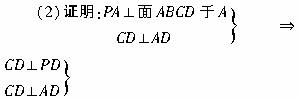
∠PDA为二面角P-CD-B的平面角
∠PDA=45°?
?
AF⊥FD.?
CD⊥平面PAD
CD⊥AF,?
.
(3)解析：由(2)知面PCE⊥面PCD,交线为PC.若作FH⊥PC于H,则FH⊥面PCE,即为所求.?
∵AD=2,∴PD=2
=CD.?
则∠CPD=45°,?
∵PF=
PD=
,?
∴FH=1.∴所求距离为1.
练习册系列答案
考前必练系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=