题目内容
(20)在1与2之间插入(Ⅰ)求数列![]() 和
和![]() 的通项;
的通项;
(Ⅱ)当![]() 时,比较
时,比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
(20)本小题主要考查等差数列、等比数列的基础知识,考查观察、猜想并进行证明的数学思想方法.
解:
(I)∵![]() 成等比数列,
成等比数列,
∴![]() ,
,
∴![]()
∴![]()
∵![]() 成等差数列,∴
成等差数列,∴![]() ,
,
∴![]()
所以,数列![]() 的通项
的通项![]() ,数列
,数列![]() 的通项
的通项![]()
(II)∵![]() ,
,![]() ,
,
∴![]() ,
,
要比较![]() 与
与![]() 的大小,只需比较
的大小,只需比较![]() 与
与![]() 的大小,也即比较当n
的大小,也即比较当n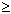 7时,
7时,![]() 与
与![]() 的大小.
的大小.
当n=7时,![]() ,
,![]() ,得知
,得知![]() ,
,
经验证![]() 时,均有命题
时,均有命题![]() 成立.
成立.
猜想当![]() 时有
时有![]() .用数学归纳法证明.
.用数学归纳法证明.
(i)当![]() 时,已验证
时,已验证![]() ,命题成立.
,命题成立.
(ii)假设![]() 时,命题成立,即
时,命题成立,即
![]() ,
,
那么 ![]()
又当![]() 时,有
时,有![]()
∴![]()
![]()
这就是说,当![]() 时,命题
时,命题![]() 成立.
成立.
根据(i)、(ii),可知命题对于![]() 都成立.
都成立.
故当![]() 时,
时,![]()

练习册系列答案
相关题目
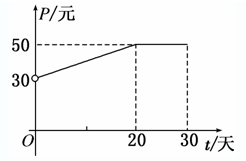 根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示. 有一个数据运算装置,如下图所示,输入数据x通过这个运算装置就输出一个数据y,输入一组数据,则会输出另一组数据.要使输入的数据介于20~100之间(含20和100,且一个都不能少),输出的另一组数据后满足下列要求:①新数据在60~100之间(含60和100,也一个都不能少);②新数据的大小关系与原数据的大小关系相反,即原数据较大的对应新数据较小.
有一个数据运算装置,如下图所示,输入数据x通过这个运算装置就输出一个数据y,输入一组数据,则会输出另一组数据.要使输入的数据介于20~100之间(含20和100,且一个都不能少),输出的另一组数据后满足下列要求:①新数据在60~100之间(含60和100,也一个都不能少);②新数据的大小关系与原数据的大小关系相反,即原数据较大的对应新数据较小.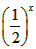 的图像上,且数列{an}是a1=1,公差为d的等差数列。
的图像上,且数列{an}是a1=1,公差为d的等差数列。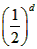 的等比数列;
的等比数列;