题目内容
函数f(x)=xcosx在区间[0,2 ]上的零点个数为
]上的零点个数为
| A.2 | B.3 | C.4 | D.5 |
B
解析试题分析:考虑到函数y=cosx的零点一定也是函数f(x)的零点,故在区间[0,2π]上y=cosx的零点有2个,结合选项可知结论。
解:因为:∵y=cosx在[0,2π]上有2零点分别为 ,那么可知函数y=x的零点有0,因此可知函数函数f(x)=xcosx在区间[0,2
,那么可知函数y=x的零点有0,因此可知函数函数f(x)=xcosx在区间[0,2 ]上的零点个数为3个,选B.
]上的零点个数为3个,选B.
考点:函数零点的运用
点评:本题主要考查了函数零点的意义和判断方法,三角函数的图象和性质,排除法解选择
题,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数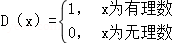 则下列结论错误的是( )
则下列结论错误的是( )
| A.D(x)的值域{0,1} | B.D(x)是偶函数 |
| C.D(x)不是周期函数 | D.D(x)不是单调函数 |
在用二分法求方程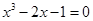 的一个近似解时,现在已经将一根锁定在(1,2)内,则下一步可断定该根所在的区间为( )
的一个近似解时,现在已经将一根锁定在(1,2)内,则下一步可断定该根所在的区间为( )
| A.(1.4,2) | B.(1,1.4) | C.(1,1.5) | D.(1.5,2) |
设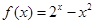 ,则在下列区间中使函数
,则在下列区间中使函数 有零点的区间是( )
有零点的区间是( )
A.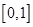 | B.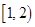 | C.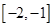 | D.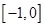 |
若函数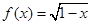 的定义域为A,函数
的定义域为A,函数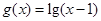 ,
,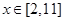 的值域为B,则
的值域为B,则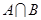 为
为
A.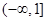 | B.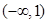 | C.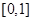 | D.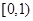 |
设 ,则
,则 =
=
| A.1 | B.2 | C.4 | D.8 |
函数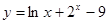 的零点一定位于区间( )
的零点一定位于区间( )
A.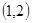 | B.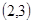 | C.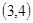 | D.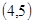 |
 的定义域是
的定义域是 ,则函数
,则函数 的定义域是 ( )
的定义域是 ( ) B.
B.  D.
D. 
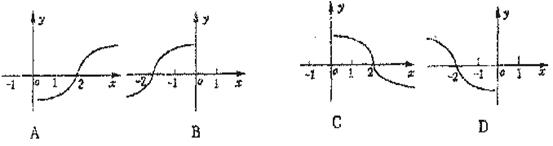
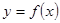 的曲线如图所示,那么方程
的曲线如图所示,那么方程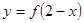 的曲线是( )
的曲线是( )