题目内容
已知方程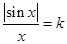 在
在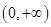 上有两个不同的解
上有两个不同的解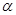 、
、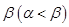 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.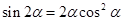 B.
B.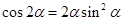
C.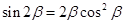 D.
D.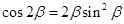
【答案】
C
【解析】
试题分析:由于方程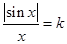 在
在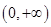 上有两个不同的解
上有两个不同的解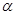 、
、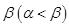 ,即方程
,即方程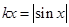 在
在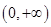 上有两个不同的解
上有两个不同的解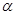 、
、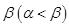 ,也就是说,直线
,也就是说,直线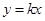 与函数
与函数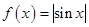 在
在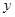 轴右侧的图象有且仅有两个交点,由图象可知,当
轴右侧的图象有且仅有两个交点,由图象可知,当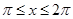 时,直线
时,直线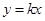 与曲线
与曲线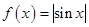 相切,且切点的横坐标为
相切,且切点的横坐标为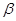 ,
,

当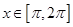 时,
时,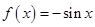 ,则
,则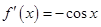 ,故
,故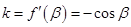 ,在切点处有
,在切点处有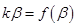
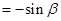 ,即
,即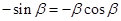 ,
,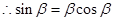 ,两边同时乘以
,两边同时乘以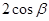 得,
得,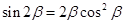 ,故选C.
,故选C.
考点:1.函数的零点;2.函数的图象;3.利用导数求切线的斜率

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
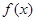 是定义在区间
是定义在区间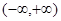 上的偶函数,且满足
上的偶函数,且满足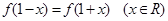
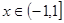 时,
时,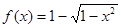 .求使方程
.求使方程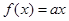 在
在 的取值集合M.
的取值集合M.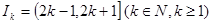 ,
,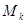 表示使方程
表示使方程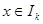 上有两个不相等实根的
上有两个不相等实根的 且关于
且关于 的方程
的方程 在
在 上有两个不相等的实数根.⑴求
上有两个不相等的实数根.⑴求 的解析式.⑵若
的解析式.⑵若 总有
总有 成立,求
成立,求 的最大值.
的最大值. ,其中
,其中 是常数.
是常数. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; ,使得关于
,使得关于 的方程
的方程 在
在 上有两个不相等的实数根,求
上有两个不相等的实数根,求