题目内容
已知函数f(x)=2cos2x+2 sinxcosx
sinxcosx
①求函数f(x)的最小正周期;
②在△ABC中,a,b,c为内角A,B,C的对边,若f(C)=2,a+b=4,求△ABC的最大面积.
解:①由已知f(x)=2cos2x+2 sinxcosx
sinxcosx
=cos2x+1+ sin2x
sin2x
=2sin(2x+ )+1
)+1
∴ …(6分)
…(6分)
②由①知 ,即
,即
又0<C<π
∴ <2C+
<2C+
∴
∴
∴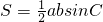 =
= =
=
当且仅当a=b时,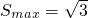 …(12分)
…(12分)
分析:①利用二倍角公式及辅助角公式对已知函数化简可得,f(x)=2sin(2x+ )+1,利用周期公式T=
)+1,利用周期公式T= 可求
可求
②由①知 ,即
,即 ,又0<C<π 可求C=
,又0<C<π 可求C=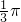 ,代入三角形的面积公式
,代入三角形的面积公式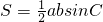 =
= 可求面积的最大值
可求面积的最大值
点评:本题主要考查了三角函数的二倍角公式、辅助角公式在三角函数化简中的应用,由三角函数值求角,基本不等式在函数最值求解中的应用.
 sinxcosx
sinxcosx=cos2x+1+
 sin2x
sin2x=2sin(2x+
 )+1
)+1∴
 …(6分)
…(6分)②由①知
 ,即
,即
又0<C<π
∴
 <2C+
<2C+
∴

∴

∴
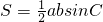 =
= =
=
当且仅当a=b时,
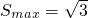 …(12分)
…(12分)分析:①利用二倍角公式及辅助角公式对已知函数化简可得,f(x)=2sin(2x+
 )+1,利用周期公式T=
)+1,利用周期公式T= 可求
可求②由①知
 ,即
,即 ,又0<C<π 可求C=
,又0<C<π 可求C=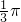 ,代入三角形的面积公式
,代入三角形的面积公式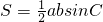 =
= 可求面积的最大值
可求面积的最大值点评:本题主要考查了三角函数的二倍角公式、辅助角公式在三角函数化简中的应用,由三角函数值求角,基本不等式在函数最值求解中的应用.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目