题目内容
设函数f(x)=lnx+x2+ax.
(Ⅰ)若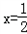 时,f(x)取得极值,求a的值;
时,f(x)取得极值,求a的值;
(Ⅱ)若f(x)在其定义域内为增函数,求a的取值范围;
(Ⅲ)设g(x)=f(x)﹣x2+1,当a=﹣1时,证明g(x)≤0在其定义域内恒成立,并证明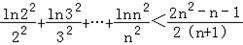 (n∈N,n≥2).
(n∈N,n≥2).
(Ⅰ)若
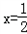 时,f(x)取得极值,求a的值;
时,f(x)取得极值,求a的值;(Ⅱ)若f(x)在其定义域内为增函数,求a的取值范围;
(Ⅲ)设g(x)=f(x)﹣x2+1,当a=﹣1时,证明g(x)≤0在其定义域内恒成立,并证明
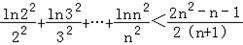 (n∈N,n≥2).
(n∈N,n≥2).解: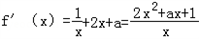 ,
,
(Ⅰ)因为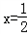 时,f(x)取得极值,所以
时,f(x)取得极值,所以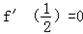 ,
,
即2+1+a=0,故a=﹣3.
(Ⅱ)f(x)的定义域为(0,+∞).
方程2x2+ax+1=0的判别式△=a2-8,
(1)当△≤0,即 时,2x2+ax+1≥0,f'(x)≥0在(0,+∞)内恒成立,此时f(x)为增函数.
时,2x2+ax+1≥0,f'(x)≥0在(0,+∞)内恒成立,此时f(x)为增函数.
(2)当△>0,即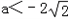 或
或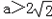 时,
时,
要使f(x)在定义域(0,+∞)内为增函数,
只需在(0,+∞)内有2x2+ax+1≥0即可,
设h(x)=2x2+ax+1,
由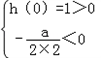 得a>0,所以
得a>0,所以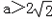 .
.
由(1)(2)可知,若f(x)在其定义域内为增函数,a的取值范围是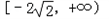 .
.
(Ⅲ)证明:g(x)=lnx+ax+1,当a=﹣1时,g(x)=lnx﹣x+1,其定义域是(0,+∞),
令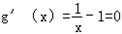 ,得x=1.则g(x)在x=1处取得极大值,也是最大值.
,得x=1.则g(x)在x=1处取得极大值,也是最大值.
而g(1)=0.所以g(x)≤0在(0,+∞)上恒成立.因此lnx≤x﹣1.
因为n∈N,n≥2,所以lnn2≤n2﹣1.则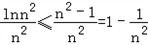 .
.
所以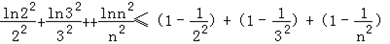 =
=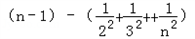 <
<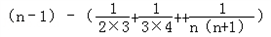 =
=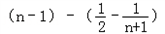 =
=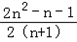 .
.
所以结论成立.
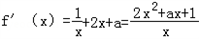 ,
,(Ⅰ)因为
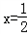 时,f(x)取得极值,所以
时,f(x)取得极值,所以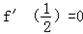 ,
,即2+1+a=0,故a=﹣3.
(Ⅱ)f(x)的定义域为(0,+∞).
方程2x2+ax+1=0的判别式△=a2-8,
(1)当△≤0,即
 时,2x2+ax+1≥0,f'(x)≥0在(0,+∞)内恒成立,此时f(x)为增函数.
时,2x2+ax+1≥0,f'(x)≥0在(0,+∞)内恒成立,此时f(x)为增函数.(2)当△>0,即
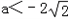 或
或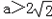 时,
时,要使f(x)在定义域(0,+∞)内为增函数,
只需在(0,+∞)内有2x2+ax+1≥0即可,
设h(x)=2x2+ax+1,
由
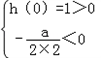 得a>0,所以
得a>0,所以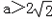 .
.由(1)(2)可知,若f(x)在其定义域内为增函数,a的取值范围是
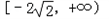 .
.(Ⅲ)证明:g(x)=lnx+ax+1,当a=﹣1时,g(x)=lnx﹣x+1,其定义域是(0,+∞),
令
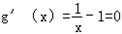 ,得x=1.则g(x)在x=1处取得极大值,也是最大值.
,得x=1.则g(x)在x=1处取得极大值,也是最大值.而g(1)=0.所以g(x)≤0在(0,+∞)上恒成立.因此lnx≤x﹣1.
因为n∈N,n≥2,所以lnn2≤n2﹣1.则
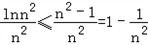 .
.所以
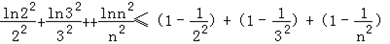 =
=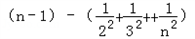 <
<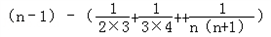 =
=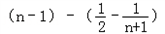 =
=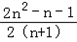 .
.所以结论成立.

练习册系列答案
相关题目