题目内容
已知函数 .若
.若 ,且
,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
C
解析试题分析:由题意f(a)=f(b),求出ab的关系,然后利用“对勾”函数的性质知函数f(a)在a∈(0,1)上为减函数,,确定a+2b的取值范围.解:因为f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或b=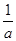 ,所以a+2b=a+
,所以a+2b=a+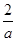 ,又0<a<b,所以0<a<1<b,令f(a)=a+
,又0<a<b,所以0<a<1<b,令f(a)=a+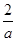 ,由“对勾”函数的性质知函数f(a)在a∈(0,1)上为减函数,所以f(a)>f(1)=1+2=3,即a+2b的取值范围是(3,+∞).故选C.
,由“对勾”函数的性质知函数f(a)在a∈(0,1)上为减函数,所以f(a)>f(1)=1+2=3,即a+2b的取值范围是(3,+∞).故选C.
考点:对数函数的性质
点评:本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a的取值范围,而利用均值不等式求得a+2b=a+ 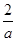 >2
>2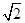 ,从而错选A,这也是命题者的用苦良心之处.
,从而错选A,这也是命题者的用苦良心之处.

练习册系列答案
相关题目
若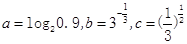 ,
,
A. | B. |
C. | D. |
已知 ,
, =( )
=( )
A. | B.0 | C.1 | D.2 |
设 ,且
,且 ,则
,则
A. | B.10 | C.20 | D.100 |
设 ,则( )
,则( )
A. | B. | C. | D. |
不等式 的解集为
的解集为 ,那么 ( )
,那么 ( )
A. | B. | C. | D. |
已知 ,则f(3)为 ( )
,则f(3)为 ( )
| A.2 | B. 3 | C. 4 | D.5 |
函数 的零点个数为( )
的零点个数为( )
| A.0 | B.1 | C.2 | D.3 |
已知函数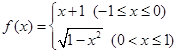 , 则
, 则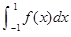 的值为
的值为
A. | B.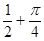 | C.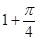 | D.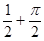 |