题目内容
已知函数f（x）=|log
x|，若m＜n，有f（m）=f（n），则m+3n的取值范围是（ ）
| 1 |
| 2 |
A、[2
| ||
B、（2
| ||
| C、[4，+∞） | ||
| D、（4，+∞） |
分析：作出f（x）的图象，由图象可知0＜m＜1＜n，由f（m）=f（n）可得m=
，从而m+3n可化为关于n的函数，用导数可判断其单调性，从而可得答案．
| 1 |
| n |
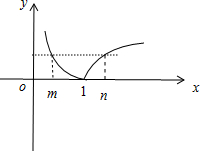
解答：解：作出f（x）=|log
x|的图象，如图所示：
∵m＜n，且f（m）=f（n），由图象可知，0＜m＜1＜n，
∴|log
m|=|log
n|，即log
m=-log
n=log
，
∴m=
，
∴m+3n=
+3n，
令g（n）=
+3n（n＞1），则g'（n）=-
+3=
＞0，
∴g（n）在（1，+∞）上递增，
∴g（n）＞g（1）=4，即m+3n的取值范围是（4，+∞），
故选：D．
| 1 |
| 2 |
∵m＜n，且f（m）=f（n），由图象可知，0＜m＜1＜n，
∴|log
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n |
∴m=| 1 |
| n |
∴m+3n=
| 1 |
| n |
令g（n）=
| 1 |
| n |
| 1 |
| n2 |
| 3n2-1 |
| n2 |
∴g（n）在（1，+∞）上递增，
∴g（n）＞g（1）=4，即m+3n的取值范围是（4，+∞），
故选：D．
点评：本题考查对数函数的图象和性质，考查函数思想，考查学生分析解决问题的能力．
练习册系列答案
导学教程高中新课标系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|