题目内容
已知数列{an}满足a1=1,且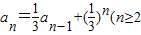 ,且n∈N*),则数列{an}的通项公式为( )
,且n∈N*),则数列{an}的通项公式为( )A.an=
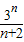
B.an=
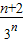
C.an=n+2
D.an=(n+2)3n
【答案】分析:由题意及足a1=1,且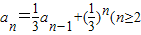 ,且n∈N*),则构造新的等差数列进而求解.
,且n∈N*),则构造新的等差数列进而求解.
解答:解:因为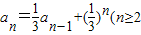 ,且n∈N*)?
,且n∈N*)?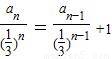 ,
,
即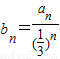 ,则数列{bn}为首项
,则数列{bn}为首项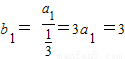 ,公差为1的等差数列,
,公差为1的等差数列,
所以bn=b1+(n-1)×1=3+n-1=n+2,所以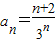 ,
,
故答案为:B
点评:此题考查了构造新的等差数列,等差数列的通项公式.
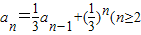 ,且n∈N*),则构造新的等差数列进而求解.
,且n∈N*),则构造新的等差数列进而求解.解答:解:因为
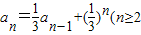 ,且n∈N*)?
,且n∈N*)?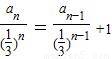 ,
,即
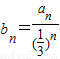 ,则数列{bn}为首项
,则数列{bn}为首项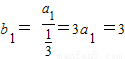 ,公差为1的等差数列,
,公差为1的等差数列,所以bn=b1+(n-1)×1=3+n-1=n+2,所以
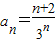 ,
,故答案为:B
点评:此题考查了构造新的等差数列,等差数列的通项公式.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目