题目内容
已知平面向量 与
与 的夹角θ∈[60°,120°],且
的夹角θ∈[60°,120°],且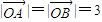 ,
, ,则
,则 的取值范围是 .
的取值范围是 .
【答案】分析:根据向量 与
与 的模长和夹角的范围,结合数量积公式得
的模长和夹角的范围,结合数量积公式得 •
• 的取值范围.再将向量
的取值范围.再将向量 平方,由数量积
平方,由数量积 •
• 的取值范围得
的取值范围得 2的范围,最后开方即可得到,
2的范围,最后开方即可得到, 的取值范围.
的取值范围.
解答:解:∵ •
• =
= =9cosθ,cosθ∈[cos120°,cos60°],
=9cosθ,cosθ∈[cos120°,cos60°],
∴ •
• 的取值范围是[-
的取值范围是[- ,
, ]
]
∵ ,
,
∴ =1+
=1+
 •
• +4=5+
+4=5+
 •
•
∵ •
• ∈[-
∈[- ,
, ],
],
∴当 •
• =-
=- 时,
时, 有最小值3;当
有最小值3;当 •
• =
= 时,
时, 有最大值7
有最大值7
因此, 的最小值是
的最小值是 ,最大值为
,最大值为
故答案为:[ ,
, ]
]
点评:本题给出两个向量的长度和夹角的范围,求它们的一个线性组合的长度取值范围,考查了平面向量数量积、模与夹角的公式等知识,属于基础题.
 与
与 的模长和夹角的范围,结合数量积公式得
的模长和夹角的范围,结合数量积公式得 •
• 的取值范围.再将向量
的取值范围.再将向量 平方,由数量积
平方,由数量积 •
• 的取值范围得
的取值范围得 2的范围,最后开方即可得到,
2的范围,最后开方即可得到, 的取值范围.
的取值范围.解答:解:∵
 •
• =
= =9cosθ,cosθ∈[cos120°,cos60°],
=9cosθ,cosθ∈[cos120°,cos60°],∴
 •
• 的取值范围是[-
的取值范围是[- ,
, ]
]∵
 ,
,∴
 =1+
=1+
 •
• +4=5+
+4=5+
 •
•
∵
 •
• ∈[-
∈[- ,
, ],
],∴当
 •
• =-
=- 时,
时, 有最小值3;当
有最小值3;当 •
• =
= 时,
时, 有最大值7
有最大值7因此,
 的最小值是
的最小值是 ,最大值为
,最大值为
故答案为:[
 ,
, ]
]点评:本题给出两个向量的长度和夹角的范围,求它们的一个线性组合的长度取值范围,考查了平面向量数量积、模与夹角的公式等知识,属于基础题.

练习册系列答案
相关题目
 与
与 的夹角为60o,且满足
的夹角为60o,且满足 ,若
,若 =1,则
=1,则 =( )
=( )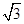 C.1 D.
C.1 D.
 与
与 的夹角为60°,且满足(
的夹角为60°,且满足( )
)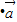 =0,若
=0,若 =1,则
=1,则 =( )
=( )

 与
与 的夹角为120°,|
的夹角为120°,| |=5,|
|=5,| |=8,则|
|=8,则| +
+ |= .
|= .