题目内容
已知M(4,0),N(1,0),若动点P满足| MN |
| MP |
| PN |
(1)求动点P的轨迹C的方程;
(2)设过点N的直线l交轨迹C于A,B两点,若-
| 18 |
| 7 |
| NA |
| NB |
| 12 |
| 5 |
分析:(1)设动点P(x,y),由已知得-3(x-4)=6
,由此得到点P的轨迹C的方程.
(2)设过N的直线l的方程为y=k(x-1),A(x1,y1),B(x2,y2),由
,得(2+4k)2x2-8k2x+4k2-12=0,再由题设条件结合根与系数的关系进行求解.
| (1-x)2+(-y)2 |
(2)设过N的直线l的方程为y=k(x-1),A(x1,y1),B(x2,y2),由
|
解答:解:(1)设动点P(x,y),
则
=(x-4,y),
=(-3,0),
=(1-x,-y)(2分)
由已知得-3(x-4)=6
,化简得3x2+4y2=12,即
+
=1
∴点P的轨迹是椭圆
+
=1(6分)
(Ⅱ)设过N的直线l的方程为y=k(x-1),A(x1,y1),B(x2,y2)
由
,得(3+4k2)x2-8k2x+4k2-12=0(8分)
∵N在椭圆内,∴△>0,∴
(10分)
∵
•
=(x1-1)(x2-1)+y1y2=(1+k2)(x1-1)(x2-1)=(1+k2)[x1x2-(x1+x2)+1]=(1+k2)
=
(12分)
∴-
≤
≤-
得1≤k2≤3
∴-
≤k≤-1或1≤k≤
(14分)
则
| MP |
| MN |
| PN |
由已知得-3(x-4)=6
| (1-x)2+(-y)2 |
| x2 |
| 4 |
| y2 |
| 3 |
∴点P的轨迹是椭圆
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设过N的直线l的方程为y=k(x-1),A(x1,y1),B(x2,y2)
由
|
∵N在椭圆内,∴△>0,∴
|
∵
| NA |
| NB |
| 4k2-12-8k2+3+4k2 |
| 3+4k2 |
| -9(1+k2) |
| 3+4k2 |
∴-
| 18 |
| 7 |
| -9(1+k2) |
| 3+4k2 |
| 12 |
| 5 |
得1≤k2≤3
∴-
| 3 |
| 3 |
点评:本题考查轨迹方程和直线与圆锥曲线的位置关系,解题时要认真审题,注意计算能力的培养.

练习册系列答案
相关题目
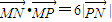 .
.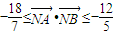 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.