题目内容
若点P是以F1，F2为焦点的双曲线
上一点，满足PF1⊥PF2，且|PF1|=2|PF2|，则此双曲线的离心率为 ．
【答案】分析：由于|PF1|=2|PF2|故点P是靠近F2的那一支上的一点则可根据双曲线的定义可得|PF1|-|PF2|=2a再结合|PF1|=2|PF2|求出
|PF1|，|PF2|的值然后再根据PF1⊥PF2可得
即可得出关于a，c的关系式从而可求出离心率e=
．
解答：解：∵|PF1|=2|PF2|
∴|PF1|-|PF2|=2a
∴|PF1|=4a，|PF2|=2a
∵PF1⊥PF2，F1F2=2c
∴
∴c2=5a2
∴e=
故答案为
点评：本题主要考察了双曲线的离心率的求解，属中档题，较难．解题的关键是抓住要求离心率即根据题中条件建立关于a，b，c的关系式！
|PF1|，|PF2|的值然后再根据PF1⊥PF2可得
即可得出关于a，c的关系式从而可求出离心率e=．解答：解：∵|PF1|=2|PF2|
∴|PF1|-|PF2|=2a
∴|PF1|=4a，|PF2|=2a
∵PF1⊥PF2，F1F2=2c
∴
∴c2=5a2
∴e=
故答案为
点评：本题主要考察了双曲线的离心率的求解，属中档题，较难．解题的关键是抓住要求离心率即根据题中条件建立关于a，b，c的关系式！
练习册系列答案
相关题目
-
=1上的一点，且|PF1|=12,则|PF2|等于( )
＋
＝1(a＞b＞0)上一点，且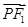
·
＝0，tan∠PF1F2＝
则此椭圆的离心率e＝（ ）
B、
C、
D、
-
=1上的一点，且|PF1|=12,则|PF2|等于( )