题目内容
 如图是一个算法的流程图,最后输出的T=
如图是一个算法的流程图,最后输出的T=-2
-2
.分析:根据流程图可知,计算出T,从而求出周期,判定是否满足I≥2010,不满足则循环,直到满足就跳出循环,最后求出T值即可.
解答:解:由流程图知,第一次循环:i=1,T=3;不满足I≥2010
第二次循环:i=2,T=-2;不满足I≥2010
第三次循环:i=3,T=-
;不满足I≥2010
第四次循环:i=4,T=
;不满足I≥2010
第五次循环:i=5,T=3;不满足I≥2010
第六次循环:i=6,T=-2;不满足I≥2010
可知周期为4,则当i=2010,T=-2满足I≥2010
此时跳出循环,∴T=-2.
故答案为:-2
第二次循环:i=2,T=-2;不满足I≥2010
第三次循环:i=3,T=-
| 1 |
| 3 |
第四次循环:i=4,T=
| 1 |
| 2 |
第五次循环:i=5,T=3;不满足I≥2010
第六次循环:i=6,T=-2;不满足I≥2010
可知周期为4,则当i=2010,T=-2满足I≥2010
此时跳出循环,∴T=-2.
故答案为:-2
点评:本题主要考查了直到型循环结构,循环结构有两种形式:当型循环结构和直到型循环结构,当型循环是先判断后循环,直到型循环是先循环后判断,属于基础题.

练习册系列答案
相关题目
 下表是某工厂10个车间2011年3月份产量的统计表,1到10车间的产量依次记为A1,A2,…,A10(如:A6表示6号车间的产量为980件).图2是统计下表中产量在一定范围内车间个数的一个算法流程图.那么算法流程(图2)输出的结果是( ) 下表是某工厂10个车间2011年3月份产量的统计表,1到10车间的产量依次记为A1,A2,…,A10(如:A6表示6号车间的产量为980件).图2是统计下表中产量在一定范围内车间个数的一个算法流程图.那么算法流程(图2)输出的结果是( )
|
下表是某工厂10个车间2011年3月份产量的统计表,1到10车间的产量依次记为 (如:
(如: 表示6号车间的产量为980件),图2是统计下表中产量在一定范围内车间个数的一个算法流程图,那么算法流程(图2)输出的结果是( ).
表示6号车间的产量为980件),图2是统计下表中产量在一定范围内车间个数的一个算法流程图,那么算法流程(图2)输出的结果是( ).
|
车间 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
产量 |
1080 |
900 |
930 |
850 |
1500 |
980 |
960 |
900 |
830 |
1250 |
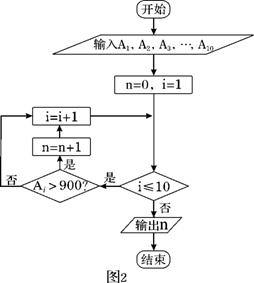
A. 5 B.6 C. 4 D. 7
下表是某工厂10个车间2011年3月份产量的统计表,1到10车间的产量依次记为 (如:
(如: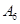 表示6号车间的产量为980件).图2是统计下表中产量在一定范围内车间个数的一个算法流程图.那么算法流程(图2)输出的结果是( )[来源:ZXXK]
表示6号车间的产量为980件).图2是统计下表中产量在一定范围内车间个数的一个算法流程图.那么算法流程(图2)输出的结果是( )[来源:ZXXK]
|
车间 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
产量 |
1080 |
900 |
930 |
850 |
1500 |
980 |
960 |
900 |
830 |
1250 |

A. 5 B. 6 C. 4 D. 7
 12、图1是某工厂2009年9月份10个车间产量统计条形图,条形图从左到右表示各车间的产量依次记为A1,A2…,A10(如A3表示3号车间的产量为950件).图2是统计图1中产量在一定范围内车间个数的一个算法流程图.那么运行该算法流程后输出的结果是
12、图1是某工厂2009年9月份10个车间产量统计条形图,条形图从左到右表示各车间的产量依次记为A1,A2…,A10(如A3表示3号车间的产量为950件).图2是统计图1中产量在一定范围内车间个数的一个算法流程图.那么运行该算法流程后输出的结果是