题目内容
在等差数列 中,已知
中,已知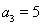 ,
,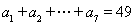 .
.
(1)求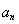 ;
;
(2)若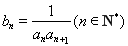 ,设数列
,设数列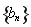 的前
的前 项和为
项和为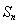 ,试比较
,试比较 与
与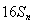 的大小.
的大小.
【答案】
(1) 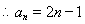 ;(2) 当
;(2) 当 时,
时,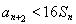 ;当
;当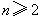 时,
时,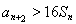 .
.
【解析】
试题分析:(1)根据等差数列的通项公式把已知转化成关于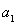 和
和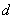 的方程,再利用公式
的方程,再利用公式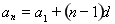 ,求出
,求出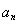 ;(2)由(1)的结果,代入得到
;(2)由(1)的结果,代入得到 ,观察形式,利用裂项相消求和,得到
,观察形式,利用裂项相消求和,得到 ,再用做差法比较
,再用做差法比较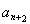 和
和 的大小,分解因式后,讨论
的大小,分解因式后,讨论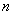 的范围,得到大小关系,此题考察等差数列的基础知识,以及求和的方法,比较大小时,不要忘记讨论
的范围,得到大小关系,此题考察等差数列的基础知识,以及求和的方法,比较大小时,不要忘记讨论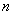 ,再比较大小,总体属于基础题型.
,再比较大小,总体属于基础题型.
试题解析:(1)由题意得: 2分
2分
解得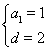 4分
4分
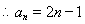 . 6分
. 6分
(2)因为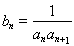 ,所以
,所以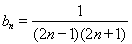 , 7分
, 7分
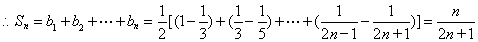 10分
10分
所以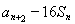 =
=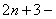
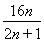 =
= , 12分
, 12分
所以当 时,
时,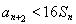 ;当
;当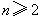 时,
时,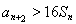 . 14分
. 14分
考点:1.等差数列的公式;2裂项相消;3.比较法.

练习册系列答案
相关题目
在等差数列中,已知a3+a5+a7=15,则3a4+a8=( )
| A、14 | B、16 | C、18 | D、20 |
 中,已知
中,已知 ,那么
,那么 等于
等于  中,已知
中,已知 ,则
,则 为 ( )
为 ( ) B.
B. C.
C. D.
D.