题目内容
△ABC的内角A、B、C的对边分别为a、b、c.若a、b、c成等比数列,且c = 2a,则cosB=( )
A.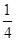 B.
B.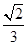 C.
C.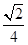 D.
D.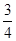
D
解析试题分析:因为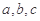 成等比数列,
成等比数列,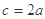 ,所以,
,所以,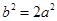 ,
,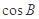 =
=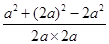 =
=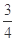 。
。
考点:本题主要考查等比数列的基础知识,余弦定理的应用。
点评:小综合题,本题较为简单,解答思路明确,先确定a,b,c关系,再应用余弦定理。

练习册系列答案
相关题目
在各项都为正数的等比数列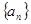 中,首项
中,首项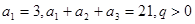 ,则
,则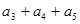 为 ( )
为 ( )
| A.21 | B.4 | C.84 | D.8 |
已知实数列-1,x,y,z,-2成等比数列,则xyz等于
| A.-4 | B.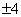 | C.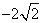 | D.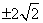 |
已知等比数列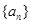 中有
中有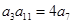 ,数列
,数列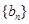 是等差数列,且
是等差数列,且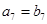 ,则
,则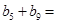
| A.2 | B.4 | C.8 | D.16 |
在各项都为正数的等比数列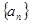 中,首项
中,首项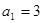 ,前三项和为21,则
,前三项和为21,则 =( )
=( )
| A.33 | B.72 | C.84 | D.189 |
已知等比数列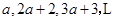 ,则第四项为( )
,则第四项为( )
A.-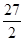 | B.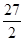 | C.-27 | D.27 |
若等比数列的首项为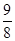 ,末项为
,末项为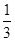 ,公比为
,公比为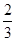 ,则这个数列的项数为( )
,则这个数列的项数为( )
| A.3 | B.4 | C.5 | D.6 |
设等比数列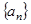 中,前n项和为
中,前n项和为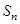 ,已知
,已知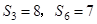 ,则
,则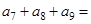
A. | B.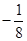 | C.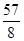 | D.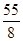 |