题目内容
(2013•临沂一模)已知O是坐标原点,点M的坐标为(2,1),若点N(x,y)为平面区域
上的一个动点,则
•
的最大值是
|
| OM |
| ON |
3
3
.分析:根据向量数量积的坐标运算公式,得
•
=2x+y.作出题中不等式组表示的平面区域得到如图的阴影部分,将目标函数z=2x+y对应的直线进行平移,可得当x=y=1时,z=2x+y达到最大值,即
•
取得最大值.
| OM |
| ON |
| OM |
| ON |
解答:解:∵M(2,1),N(x,y),∴目标函数z=
•
=2x+y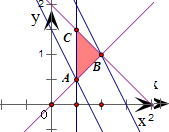
作出不等式组
表示的平面区域,
得到如图的△ABC及其内部,其中A(
,
),B(1,1),C(
,
)
设z=F(x,y)=2x+y,将直线l:z=2x+y进行平移,
当l经过点B时,目标函数z达到最大值
∴z最大值=F(1,1)=3
故答案为:3
| OM |
| ON |

作出不等式组
|
得到如图的△ABC及其内部,其中A(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
设z=F(x,y)=2x+y,将直线l:z=2x+y进行平移,
当l经过点B时,目标函数z达到最大值
∴z最大值=F(1,1)=3
故答案为:3
点评:本题给出二元一次不等式组,求目标函数z=
•
的最大值,着重考查了二元一次不等式组表示的平面区域、向量数量积的坐标运算公式和简单的线性规划等知识,属于基础题.
| OM |
| ON |

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
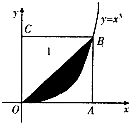 (2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )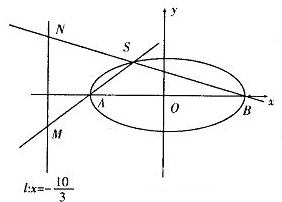 (2013•临沂一模)如图,已知椭圆C:
(2013•临沂一模)如图,已知椭圆C: