题目内容
若当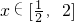 时,函数f(x)=x2+px+q与函数
时,函数f(x)=x2+px+q与函数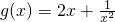 在同一点处取得相同的最小值,则函数f(x)在
在同一点处取得相同的最小值,则函数f(x)在 上的最大值是________.
上的最大值是________.
4
分析:利用基本不等式可求得g(x)=x+x+ ≥3(当x=1时取“=”),从而可求得p=-2,q=4,从而可求得f(x)在
≥3(当x=1时取“=”),从而可求得p=-2,q=4,从而可求得f(x)在 上的最大值.
上的最大值.
解答:∵x∈[ ,2],g(x)=x+x+
,2],g(x)=x+x+ ≥3(当且仅当x=1时取“=”),
≥3(当且仅当x=1时取“=”),
∵数f(x)=x2+px+q与函数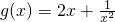 在同一点处取得相同的最小值,
在同一点处取得相同的最小值,
∴f(x)=x2+px+q在x=1处取到最小值3,而x∈[ ,2],
,2],
∴- =1,p=-2.
=1,p=-2.
∴f(1)=12-2×1+q=3,
∴q=4.
∴f(x)=x2-2x+4,
∵f(x)=x2-2x+4在[ ,1]上单调递减,在[1,2]上单调递增,且2到x=1的距离大于
,1]上单调递减,在[1,2]上单调递增,且2到x=1的距离大于 到x=1的距离,二次函数开口向上,
到x=1的距离,二次函数开口向上,
∴x∈[ ,2],f(x)max=f(2)=22-2×2+4=4.
,2],f(x)max=f(2)=22-2×2+4=4.
故答案为:4.
点评:本题考查基本不等式,通过基本不等式的应用考查二次函数在闭区间上的单调性与最值,考查分析转化与运算的能力,属于中档题.
分析:利用基本不等式可求得g(x)=x+x+
 ≥3(当x=1时取“=”),从而可求得p=-2,q=4,从而可求得f(x)在
≥3(当x=1时取“=”),从而可求得p=-2,q=4,从而可求得f(x)在 上的最大值.
上的最大值.解答:∵x∈[
 ,2],g(x)=x+x+
,2],g(x)=x+x+ ≥3(当且仅当x=1时取“=”),
≥3(当且仅当x=1时取“=”),∵数f(x)=x2+px+q与函数
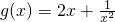 在同一点处取得相同的最小值,
在同一点处取得相同的最小值,∴f(x)=x2+px+q在x=1处取到最小值3,而x∈[
 ,2],
,2],∴-
 =1,p=-2.
=1,p=-2.∴f(1)=12-2×1+q=3,
∴q=4.
∴f(x)=x2-2x+4,
∵f(x)=x2-2x+4在[
 ,1]上单调递减,在[1,2]上单调递增,且2到x=1的距离大于
,1]上单调递减,在[1,2]上单调递增,且2到x=1的距离大于 到x=1的距离,二次函数开口向上,
到x=1的距离,二次函数开口向上,∴x∈[
 ,2],f(x)max=f(2)=22-2×2+4=4.
,2],f(x)max=f(2)=22-2×2+4=4.故答案为:4.
点评:本题考查基本不等式,通过基本不等式的应用考查二次函数在闭区间上的单调性与最值,考查分析转化与运算的能力,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 ,求函数f(x)的解析式;
,求函数f(x)的解析式; ,求b的最大值;
,求b的最大值; 为函数f(x)的一个极值点,设函数
为函数f(x)的一个极值点,设函数 ,当
,当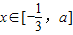 时求|g(x)|的最大值.
时求|g(x)|的最大值. .
.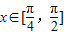 时,不等式|f(x)-m|<2恒成立,求实数m的取值范围.
时,不等式|f(x)-m|<2恒成立,求实数m的取值范围.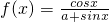 (a为实数)
(a为实数) 时,函数f(x)有极值,求a的取值范围并求此极值.
时,函数f(x)有极值,求a的取值范围并求此极值. 时,函数f(x)=x2+px+q与函数
时,函数f(x)=x2+px+q与函数 在同一点处取得相同的最小值,则函数f(x)在
在同一点处取得相同的最小值,则函数f(x)在 上的最大值是 .
上的最大值是 .